Verjetnostna porazdelitev

Najbolj pogosto uporabljana verjetnostna porazdelitev (normalna ali Gaussova porazdelitev).

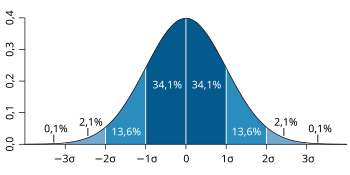
Verjetnostna porazdelitev (tudi porazdelitev verjetnosti) je v verjetnostnem računu in statistiki pravilo, ki določa verjetnost, da slučajna spremenljivka zavzame neko vrednost. Porazdelitev verjetnosti opisuje območje, ki ga slučajna spremenljivka lahko zavzame, in verjetnost, da je vrednost premeljivke v tem območju. To z drugimi besedami pomeni, da je to funkcija, ki povezuje statistični poskus in verejtnost izida tega poskusa.

Verjetnostne porazdelitve so lahko

• diskretna, kjer lahko spremenljivka zavzame samo določene vrednosti (končno število vrednosti)
• zvezne, kjer lahko spremenljivka zavzame vsako vrednost (neskončno vrednosti)

Diskretna porazdelitev

Ker je verjetnost, da spremenljivka zavzame neko vrednost, enaka

$p_i \geqslant 0$

velja

$\sum_{i=1}^{\infty}p_i = 1$

Zvezna porazdelitev

Če z $\mathbf{f(x)}$ označimo zvezno funkcijo gostote verjetnosti za katero za vsak x velja

$f(x) \geqslant 0,\; \forall x \in \mathbb{R}$;

potem je

$\int\limits_{-\infty}^{\infty} f(x)\, dx = 1$

To pomeni, da je ploščina pod krivuljo vedno enaka 1 (vsota vseh verjetnosti je 1).

Velja tudi naslednja zveza med zbirno funkcijo verjetnosti (kumulativna funkcija porazdelitve) ($\mathbf{F}$) in porazdelitvijo verjetnosti

$F'(x) = f(x),\; \forall x \in \mathbb{R},$

$F(x) = \int\limits_{-\infty}^x f(t)\, dt$

Glej tudi

• slučajna spremenljivka
• seznam verjetnostnih porazdelitev
• zbirna funkcija verjetnosti