Težiščni koordinatni sistem (tudi baricentrični koordinatni sistem) je v geometriji koordinatni sistem v katerem je lega točke določena kot masno središče mas, ki se nahajajo v ogliščih simpleksov (trikotnik , tetraeder ...). Težiščne koordinate spadajo med homogene koordinate . Koordinate ročke v težiščnem koordinatnem sistemu imenujemo težiščne koordinate .
Sistem težiščnih koordinat je prvi vpeljal nemški matematik in astronom August Ferdinand Möbius v letu 1827 .
Naj bodo
x
1
…
x
n
{\displaystyle {\textbf {x}}_{1}\ldots {\textbf {x}}_{n}}
oglišča simpleksa v vektorskem prostoru
A
{\displaystyle A\,}
in, če za neko točko
p
{\displaystyle {\textbf {p}}}
A
{\displaystyle A\,}
(
a
1
+
⋯
+
a
n
)
p
=
a
1
x
1
+
⋯
+
a
n
x
n
{\displaystyle (a_{1}+\cdots +a_{n}){\textbf {p}}=a_{1}\,{\textbf {x}}_{1}+\cdots +a_{n}\,{\textbf {x}}_{n}}
a
1
+
⋯
+
a
n
{\displaystyle a_{1}+\cdots +a_{n}\,}
V tem primeru lahko rečemo, da so koeficienti
(
a
1
+
⋯
+
a
n
)
{\displaystyle (a_{1}+\cdots +a_{n})\,}
p
{\displaystyle {\textbf {p}}}
x
1
⋯
x
n
{\displaystyle x_{1}\cdots x_{n}\,}
Oglišča imajo koordinate
x
1
=
(
1
,
0
,
0
,
.
.
.
,
0
)
,
x
2
=
(
0
,
1
,
0
,
.
.
.
,
0
)
,
…
,
x
n
=
(
0
,
0
,
0
,
.
.
.
,
1
)
{\displaystyle {\textbf {x}}_{1}=(1,0,0,...,0),{\textbf {x}}_{2}=(0,1,0,...,0),\ldots ,{\textbf {x}}_{n}=(0,0,0,...,1)}
Težiščnih koordinat ne moremo določiti enolično. Za vsak
b
{\displaystyle b\,}
(
b
a
1
,
⋯
,
b
a
n
)
{\displaystyle (ba_{1},\cdots ,ba_{n})\,}
p
{\displaystyle p\,}
P
{\displaystyle P\,}
konveksni ogrinjači za
x
1
⋯
x
n
{\displaystyle x_{1}\cdots x_{n}\,}
Težiščne koordinate
(
λ
1
,
λ
2
,
λ
3
)
{\displaystyle (\lambda _{1},\lambda _{2},\lambda _{3})}
Imamo definiran trikotnik
T
{\displaystyle T\,}
r
1
{\displaystyle r_{1}\,}
r
2
{\displaystyle r_{2}\,}
r
3
{\displaystyle r_{3}\,}
r
=
λ
1
r
1
+
λ
2
r
2
+
λ
3
r
3
,
{\displaystyle {\textbf {r}}=\lambda _{1}{\textbf {r}}_{1}+\lambda _{2}{\textbf {r}}_{2}+\lambda _{3}{\textbf {r}}_{3},}
kjer so
λ
1
,
λ
2
,
λ
3
{\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}\,}
Za te koordinate velja omejitev
λ
1
+
λ
2
+
λ
3
=
1
{\displaystyle \lambda _{1}+\lambda _{2}+\lambda _{3}=1\,}
Imamo dano točko
r
{\displaystyle r\,}
λ
1
,
λ
2
,
λ
3
{\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}\,}
Kartezičnih koordinatah
(
x
,
y
)
{\displaystyle (x,y)\,}
r
1
,
r
2
,
r
3
{\displaystyle r_{1},r_{2},r_{3}\,}
x
=
λ
1
x
1
+
λ
2
x
2
+
λ
3
x
3
y
=
λ
1
y
1
+
λ
2
y
2
+
λ
3
y
3
{\displaystyle {\begin{matrix}x=\lambda _{1}x_{1}+\lambda _{2}x_{2}+\lambda _{3}x_{3}\\y=\lambda _{1}y_{1}+\lambda _{2}y_{2}+\lambda _{3}y_{3}\\\end{matrix}}\,}
Po preureditvi lahko to napišemo kot linearno transformacijo
T
⋅
λ
=
r
−
r
3
{\displaystyle {\textbf {T}}\cdot \lambda ={\textbf {r}}-{\textbf {r}}_{3}\,}
kjer je
λ
{\displaystyle \lambda \,}
r
{\displaystyle r\,}
vektor v kartezičnih koordinatah
T
{\displaystyle T\,}
matrika , ki ima vrednost
T
=
(
x
1
−
x
3
x
2
−
x
3
y
1
−
y
3
y
2
−
y
3
)
{\displaystyle {\textbf {T}}=\left({\begin{matrix}x_{1}-x_{3}&x_{2}-x_{3}\\y_{1}-y_{3}&y_{2}-y_{3}\\\end{matrix}}\right)}
Ker sta
r
1
−
r
2
{\displaystyle r_{1}-r_{2}\,}
r
2
−
r
3
{\displaystyle r_{2}-r_{3}\,}
linearno neodvisna , je matrika
T
{\displaystyle T\,}
obrnljiva . To pomeni, da po preureditvi dobimo
(
λ
1
λ
2
)
=
T
−
1
(
r
−
r
3
)
{\displaystyle \left({\begin{matrix}\lambda _{1}\\\lambda _{2}\end{matrix}}\right)={\textbf {T}}^{-1}({\textbf {r}}-{\textbf {r}}_{3})\,}
Iz tega se dobijo težiščne koordinate
λ
1
=
(
y
2
−
y
3
)
(
x
−
x
3
)
+
(
x
3
−
x
2
)
(
y
−
y
3
)
det
(
T
)
=
(
y
2
−
y
3
)
(
x
−
x
3
)
+
(
x
3
−
x
2
)
(
y
−
y
3
)
(
y
2
−
y
3
)
(
x
1
−
x
3
)
+
(
x
3
−
x
2
)
(
y
1
−
y
3
)
,
{\displaystyle \lambda _{1}={\frac {(y_{2}-y_{3})(x-x_{3})+(x_{3}-x_{2})(y-y_{3})}{\det(T)}}={\frac {(y_{2}-y_{3})(x-x_{3})+(x_{3}-x_{2})(y-y_{3})}{(y_{2}-y_{3})(x_{1}-x_{3})+(x_{3}-x_{2})(y_{1}-y_{3})}}\,,}
λ
2
=
(
y
3
−
y
1
)
(
x
−
x
3
)
+
(
x
1
−
x
3
)
(
y
−
y
3
)
det
(
T
)
=
(
y
3
−
y
1
)
(
x
−
x
3
)
+
(
x
1
−
x
3
)
(
y
−
y
3
)
(
y
3
−
y
1
)
(
x
2
−
x
3
)
+
(
x
1
−
x
3
)
(
y
2
−
y
3
)
,
{\displaystyle \lambda _{2}={\frac {(y_{3}-y_{1})(x-x_{3})+(x_{1}-x_{3})(y-y_{3})}{\det(T)}}={\frac {(y_{3}-y_{1})(x-x_{3})+(x_{1}-x_{3})(y-y_{3})}{(y_{3}-y_{1})(x_{2}-x_{3})+(x_{1}-x_{3})(y_{2}-y_{3})}}\,,}
λ
3
=
1
−
λ
1
−
λ
2
{\displaystyle \lambda _{3}=1-\lambda _{1}-\lambda _{2}\,}
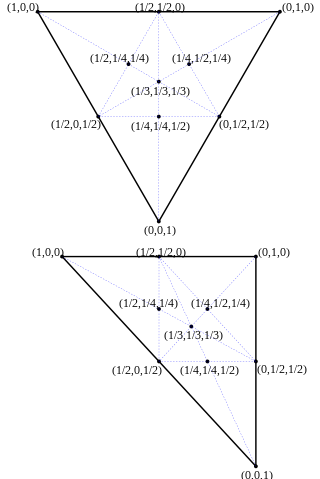
Težiščni koordinatni sistem se z lahkoto razširi na tri razsežnosti. Simpleks v treh razsežnostih je tetraeder , ki je polieder , ki ima tri trikotne stranske ploskve in štiri oglišča.
Tudi tukaj težiščni sistemdoločimo tako, da ima prvo oglišče koordinate
λ
=
(
1
,
0
,
0
,
0
)
{\displaystyle \lambda =(1,0,0,0)\,}
Tudi tukaj velja
(
λ
1
λ
2
λ
3
)
=
T
−
1
(
r
−
r
4
)
{\displaystyle \left({\begin{matrix}\lambda _{1}\\\lambda _{2}\\\lambda _{3}\end{matrix}}\right)={\textbf {T}}^{-1}({\textbf {r}}-{\textbf {r}}_{4})\,}
kjer je
T
{\displaystyle T\,}
3
×
3
{\displaystyle 3\times 3\,}
T
=
(
x
1
−
x
4
x
2
−
x
4
x
3
−
x
4
y
1
−
y
4
y
2
−
y
4
y
3
−
y
4
z
1
−
z
4
z
2
−
z
4
z
3
−
z
4
)
{\displaystyle {\textbf {T}}=\left({\begin{matrix}x_{1}-x_{4}&x_{2}-x_{4}&x_{3}-x_{4}\\y_{1}-y_{4}&y_{2}-y_{4}&y_{3}-y_{4}\\z_{1}-z_{4}&z_{2}-z_{4}&z_{3}-z_{4}\end{matrix}}\right)}
Kadar so težiščne koordinate določene glede na politop (namesto glede na simpleks), dobimo posplošene težiščne koordinate.
Še vedno mora veljati
(
a
1
+
⋯
+
a
n
)
p
=
a
1
x
1
+
⋯
+
a
n
x
n
{\displaystyle (a_{1}+\cdots +a_{n})p=a_{1}x_{1}+\cdots +a_{n}x_{n}}
kjer so
x
1
⋯
x
n
{\displaystyle x_{1}\cdots x_{n}\,}