Duoprizma

Skupina uniformnih p,q-duoprizem Primer 16,16-duoprizme Schleglov diagram Projekcija iz središča 16-strane prizme. Prikazane so vse, razen ene nasprotne 16-strane prizme.
vrsta	Prizmatični uniformni uniformni polihoron
Schläflijev simbol	{p}x{q}
Coxeter-Dinkinov diagram
celice	p q-strane prizme, q p-strane prizme
stranske ploskve	pq kvadratov, p q-strane, q p-strane
robovi	2pq
oglišča	pq
slika oglišč	disfenoidni tetraeder
simetrija	[p,2,q], reda 4pq [[p,2,p]], reda 8p2, p=q
dual	duopiramida
lastnosti	konveksni, če sta obe osnovnici konveksni

Mreža 16-16 duoprizme. Prikazani sta dve skupini 16-stranih prizem. Zgornja in spodnja stranska ploskev navpičnega valja sta povezani, če ju zvijemo in povežemo v četrti razsežnosti (4D).

Duoprizma (tudi dvojna prizma) je v geometriji štirih in višjih razsežnostih politop, ki nastane kot kartezični produkt dveh politopov. Vsak od teh dveh politopov ima razsežnost dva ali višjo. Kartezični produkt n politopa in m politopa je (n+m) politop, kjer sta n in m enaka 2 ali več. Duoprizma z najnižjo razsežnostjo je tista, ki obstoja v štirirazsežnem prostoru kot polihoron (4 politop) in je kartezični produkt dveh mnogokotnikov v dvorazsežnem evklidskem prostoru. Natančneje to zapišemo kot množico točk:

$P_{1}\times P_{2}=\{(x,y,z,w)|(x,y)\in P_{1},(z,w)\in P_{2}\}$

kjer sta P₁ in P₂ množici točk, ki pripadajo odgovarjajočima mnogokotnikoma. Takšna duoprizma je konveksna, če sta obe osnovnici konveksni in sta povezani s prizmatičnimi celicami.

Poimenovanje

Štiri razsežna duoprizma se obravnava kot prizmatičen polihoron. Duoprizma, ki jo dobimo iz dveh pravilnih mnogokotnikov z isto velikostjo je uniformna duoprizma.

Duoprizme, ki jo sestavlja n mnogokotnikov in m mnogokotnikov imenujemo tako, da spredaj uporabimo predpono 'duoprizma' in nadaljujemo z osnovnimi mnogokotniki. Zgled: tristrano-petstrana duoprizma je kartezični produkt trikotnika in petkotnika.

Drugi način, ki pa je natančnejši, je osnovan tako, da uporabimo kot predpone števila, ki označujejo osnovne mnogokotnike. Zgled: 3,5 duoprizma je tristrano-petstrana duoprizma.

Druga imena lahko imajo še oblike:

• q-strana p-strana prizma
• q-strana p-strana dvojna prizma
• q-strana p-strana hiperprizma

Izraz duoprizma je skoval svobodni izdajatelj, pisatelj in založnik ter ljubitelsjkipaleontolog in matematik George Olshevsky (rojen 1946).

Geometrija štirirazsežnih duoprizem

Pogled na notranjost 23-29 duoprizme projicirane na 3-sfero. Ko m in n postajata večja, se geometrija duoprizme približuje geometriji duocilindra tako kot se p-strana prizma približuje geometriji valja.

Štirirazsežna uniformna duoprizma nastane kot produkt pravilnega n-kotnega mnogokotnika in pravilnega m-kotnega mnogokotnika z enako dolžino robov. Omejen je z m-stranimiprizmami in n-stranimi prizmami. Zgled: kartezični produkt trikotnika in šestkotnika je duoprizma omejena s šestimi tristranimi prizmami in tremi šeststranimi prizmami.

Slike uniformnih polihoronskih duoprizem

Vse naslednje slike so Schleglovi diagrami, ki imajo prikazano samo eno celico. Duoprizme p-q so enake duoprizmam q-p. Izgledajo pa drugačne, ker so projicirane v središče druge celice.

6-prizma	6-6-duoprizma
Šeststrana prizma, projicirana na ravnino s perspektivo s središčem na šestkotniški stranski ploskvi, izgleda kot dvojni šestkotnik, povezan s (popačenimi) kvadrati. Podobno je 6-6 duoprizma projicirana na trirazsežnosti približek torusa, ki je šestkotniški v ravnini in preseku.

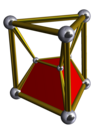3-3	3-4	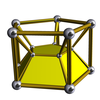3-5	3-6	3-7	3-8
4-3	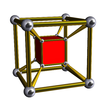4-4	4-5	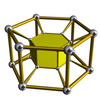4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Sorodni politopi

Stereografska projekcija vrtečega se duocilindra, divided into a checkerboard surface of squares from the {4,4|n} skew polyhedron

Pravilni poševni poliedri {4,4|n} obstojajo v štirirazsežnem prostoru kot n² kvadratne stranske ploskve n-n duoprizem, ki imajo 2n² robov in n² oglišč.

Duoantiprizme

Duoprizme , t_0,1,2,3{p,2,q}, lahko alterniramo v duoantiprizme , s{p,2,q}, ki pa v splošnem ne morajo postati uniformne. Edina konveksna uniformna rešitev je trivialni primer p=q=2, ki je konstrukcija teserakta z nižjo simetrijo , t_0,1,2,3{2,2,2}. Z alternacijo dobimo 16-celico , s{2,2,2}.

Edina nekonveksna uniformna rešitev je p=5, q=5/3, s{5,2,5/3}, ki jo konstruiramo iz desetih petstranih antiprizem in desetih pentagramskih križnih antiprizem in petdesetih tetraedrov. To telo je znano kot velika duoantiprizma (gudap) .

Politopi k_22

Duoprizme 3-3,-1₂₂ so prve v skupini uniformnih politopov, ki jih je Coxeter (1907 - 2003) označil za k₂₂ serijo. Duoprizme 3-3 so slike oglišč za drugo skupino dvojno rektificirani 5 simpleks. Četrta skupina je evklidsko satovje 2₂₂. Zadnja skupina pa je nekompaktno hiperbolično satovje 3₂₂. Vsak naslednji uniformni politop se dobi iz prejšnjega kot njegova slika oglišča.

Oblike politopov k₂₂

n	4	5	6	7	8
Coxeterjeva grupa	A22	A5	E6	${\tilde {E}}_{6}$=E6+	E6++
Coxeterjev diagram
graf				∞	∞
ime	−122	022	122	222	322

Glej tudi

• politop
• polihoron
• konveksni pravilni polihoron
• duocilinder

Zunanje povezave

• Pojasnjena četrta razsežnost (angleško)
• Raziskovanje hiperprostora (angleško)
• Duoprizma na Glossary for Hyperspace (Olshevsky)(angleško)
• (angleško)
• Konveksni uniformni prizmatični polihoroni (Olshevsky) (angleško)
• Polygloss (angleško)