Izoedrska oblika
Izoedrska oblika (tudi prehodnost (tranzitivnost) stranske ploskve) nastopi takrat, ko so vse stranske ploskve enake. To velja za politope ali tlakovanja. Pomeni pa, da stranske ploskve niso samo skladne ampak prehodnee.
Izoedrski poliedri se imenujejo izoedri. Lahko se jih opiše z njihovo konfiguracijo stranskih ploskev. Oblika, ki je izoedrska in ima pravilna oglišča, je tudi robovno prehodna. Zanjo se lahko reče, da je kvazipravilni dual.
Polieder, ki je izoedrski, ima dualni polieder, ki je ogliščno prehoden (izogonalen). Telesa, ki so izoedrska, so Catalanova telesa, bipiramide in trapezoedri. Vsi po vrsti so dualna telesa izogonalnih arhimedskih teles, prizem in antiprizem.
Zgledi[uredi | uredi kodo]
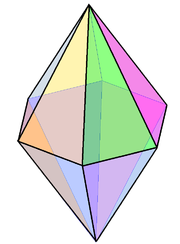 Šestkotna bipiramida, V4.4.6 je nepravilni primer izoedrskega poliedra. |
 Izoedrsko kairsko petkotno tlakovanje, V3.3.4.3.4 |
 Rombsko dodekaedersko satovje je primer izoedrskega satovja, ki zapolni prostor. |
Sorodni pojmi[uredi | uredi kodo]
Celično prehodna ali izohorna oblika je n-politop (n > 3) ali satovje, ki ima skladne in prehodne celice.
Facetno prehodna ali izotopska oblika je n-razsežni politop ali satovje s facetami ((n - 1) stranske ploskve), ki so skladne in prehodne. Duali izotopske oblike so izogonalni politopi. Po definiciji je ta izotopska značilnost skupna dualom uniformnih politopov.
- izotopska 2-razsežna oblika je izotaksalna (robovno prehodna)
- izotopska 3-razsežna oblika je izoedrska (prehodne stranske ploskve)
- izotopska 4-razsežna oblika je izohorna (celično prehodna)
