Geometrijska algebra

Geometrijska algebra (kratica GA) je multilinearna algebra, ki izhaja iz Cliffordove in Grassmannove algebre.

Značilnost geometrijske algebre je, da se njeni produkti obravnavajo na geometrijski način.

Definicija

V geometrijski algebri so za n-razsežni realni vektorski prostor določeni trije produkti dveh vektorjev ${\vec {a}}\,$ in ${\vec {b}}\,$:

• skalarni produkt ali notranji produkt, ki nam da skalar (0-vektor), za katerega velja

${\vec {a}}^{2}={\vec {a}}{\vec {a}}=\epsilon |{\vec {a}}|^{2}\ (\epsilon \in {1,0,-1})$

oziroma

${\vec {a}}\cdot {\vec {b}}={\dfrac {1}{2}}({\vec {a}}{\vec {b}}+{\vec {b}}{\vec {a}})={\vec {b}}\cdot {\vec {a}}$

Ta je enak Evklidskemu notranjemu produktu, če sta oba vektorja pozitivna.

• zunanji produkt

${\vec {a}}\wedge {\vec {b}}={\dfrac {1}{2}}({\vec {a}}{\vec {b}}-{\vec {b}}{\vec {a}})=-{\vec {b}}\wedge {\vec {a}}$, ki pa je bivektor (2-vektor)

• z združitvijo obeh zgornjih enačb, dobimo geometrijski produkt (Cliffordov produkt) (oznaka ${\vec {a}}{\vec {b}}\,$)

${\vec {a}}{\vec {b}}={\vec {a}}\cdot {\vec {b}}+{\vec {a}}\wedge {\vec {b}}$, ki je multivektor (je vsota k-vektorjev različnih stopenj, v tem primeru 0-vektorja in 2-vektorja). Za geometrijski produkt velja tudi

${\vec {a}}\cdot {\vec {b}}=1/2({\vec {a}}{\vec {b}}+{\vec {b}}{\vec {a}})\,$ in

${\vec {a}}\wedge {\vec {b}}=1/2({\vec {a}}{\vec {b}}-{\vec {b}}{\vec {a}})$.

Zakaj lahko v geometrijskem produktu seštejemo skalar in bivektor? To je podoben primer kot pri kompleksnih številih. Tudi kompleksna števila so sestavljena iz realnega in imaginarnega dela. Podobno je pri geometrijskem produktu, ki je sestavljen iz skalarnega in bivektorskega dela. Takšne kombinacije imenujemo multivektorje. V $\mathbb {R} ^{2}\,$ bo takšen multivektor vseboval skalarni del, vektorski del in bivektorski del. V $\mathbb {R} ^{2}\,$ potrebujemo 4 (2²) realnih števil, da določimo celoten multivektor. V $\mathbb {R} ^{3}\,$ potrebujemo 8 (2³) realnih števil za določitev multivektorja.

Zunanji produkt lahko posplošimo na poljubno število vektorjev

${\vec {a}}_{1}\wedge {\vec {a}}_{2}\wedge ...\wedge {\vec {a}}_{k}=A\,$,

kjer se

• $k$ imenuje stopnja $A\,$.

Zunanji produkt n vektorjev nam da psevdoskalar

Vektorski produkt v primerjavi z zunanjim produktom. Z rdečo barvo je označen enotski normalni vektor.

Primerjava geometrijske algebre z vektorsko algebro

V vektorski algebri so osnovni matematični objekti skalarji in vektorji in med njimi operaciji kot sta skalarni in vektorski produkt.

V geometrijski algebri so osnovni objekti multivektorji (0-vektorji so skalarji, 1-vektorji so običajni vektorji), kot operacije pa se uporabljajo skalarni in vektorski ter geometrijski produkt, ki pa je vsota notranjega in zunanjega produkta.

Vektorska algebra uporablja vektorski produkt, geometrijska algebra pa uporablja zunanji produkt. V Evklidskem 3-razsežnem prostoru geometrijska algebra loči 0-vektorje, 1-vektorje, 2-vektorje ter 3-vektorje. Vektorska algebra pa pozna 1-vektorje in 2-vektorje kot vektorje in 0-vektorje ter 3-vektorje kot skalarje. Vsi ti objekti so znani tudi kot skalarji, vektorji, psevdovektorji in psevdoskalarji.

Vektorski in zunanji produkt sta antisimetrična:

${\vec {\mathbf {v} }}\times {\vec {\mathbf {u} }}=-({\vec {\mathbf {u} }}\times {\vec {\mathbf {v} }})\,$

${\vec {\mathbf {v} }}\wedge {\vec {\mathbf {u} }}=-({\vec {\mathbf {u} }}\wedge {\vec {\mathbf {v} }})\,$

Sta tudi linearna v prvem operandu

$({\vec {\mathbf {u} }}+{\vec {\mathbf {v} }})\times {\vec {\mathbf {w} }}={\vec {\mathbf {u} }}\times {\vec {\mathbf {w} }}+{\vec {\mathbf {v} }}\times {\vec {\mathbf {w} }}\,$

$({\vec {\mathbf {u} }}+{\vec {\mathbf {v} }})\wedge {\vec {\mathbf {w} }}={\vec {\mathbf {u} }}\wedge {\vec {\mathbf {w} }}+{\vec {\mathbf {v} }}\wedge {\vec {\mathbf {w} }}\,$

in v drugem operandu

${\vec {\mathbf {u} }}\times ({\vec {\mathbf {v} }}+{\vec {\mathbf {w} }})={\vec {\mathbf {u} }}\times {\vec {\mathbf {v} }}+{\vec {\mathbf {u} }}\times \mathbf {w} \,$

${\vec {\mathbf {u} }}\wedge ({\vec {\mathbf {v} }}+{\vec {\mathbf {w} }})={\vec {\mathbf {u} }}\wedge {\vec {\mathbf {v} }}+{\vec {\mathbf {u} }}\wedge {\vec {\mathbf {w} }}\,$

Vektorski produkt ni asociativen, zunanji produkt pa je

$({\vec {\mathbf {u} }}\times {\vec {\mathbf {v} }})\times {\vec {\mathbf {w} }}\neq \mathbf {u} \times ({\vec {\mathbf {v} }}\times {\vec {\mathbf {w} }})\,$

$({\vec {\mathbf {u} }}\wedge {\vec {\mathbf {v} }})\wedge {\vec {\mathbf {w} }}={\vec {\mathbf {u} }}\wedge ({\vec {\mathbf {v} }}\wedge {\vec {\mathbf {w} }})\,$

kjer je

• ${\vec {\mathbf {u} }}\times {\vec {\mathbf {v} }}$ pravokoten na ravnino, ki vsebuje ${\vec {\mathbf {u} }}$ in ${\vec {\mathbf {v} }}$.
  
• ${\vec {\mathbf {u} }}\wedge {\vec {\mathbf {v} }}$ orientirani prikaz iste ravnine.

Vektorski in zunanji produkt dveh enakih vektorjev je nič

${\vec {\mathbf {u} }}\times {\vec {\mathbf {u} }}=0$

${\vec {\mathbf {u} }}\wedge {\vec {\mathbf {u} }}=0$

Baze in bivektorji

Za skupino ortonormiranih vektorjev ${\vec {\sigma }}_{1},{\vec {\sigma }}_{2}\dots ,\,$ lahko zapišemo

${\vec {\sigma }}_{i}\cdot {\vec {\sigma }}_{j}=1/2({\vec {\sigma }}_{i}{\vec {\sigma }}_{j})=\delta _{ij}\,$

kjer je

• $\delta _{ij}\,$ Kroneckerjeva delta.

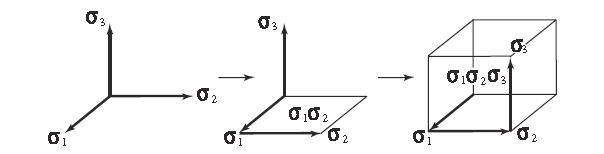
Velja tudi

${\vec {\sigma }}_{1}\wedge {\vec {\sigma }}_{1}=0\,$

in

${\vec {\sigma }}_{2}\wedge {\vec {\sigma }}_{2}=0\,$.

Enotski bivektor $i\,$ za ravnino, ki vsebuje ${\vec {\sigma }}_{1}\,$ in ${\vec {\sigma }}_{2}\,$, je določen s produktom

$i={\vec {\sigma }}_{1}{\vec {\sigma }}_{2}={\vec {\sigma }}_{1}\wedge {\vec {\sigma }}_{2}=-{\vec {\sigma }}_{2}{\vec {\sigma }}_{1}\,$.

Pri tem velja pomembna zveza $i^{2}=-1\,$, kar pomeni, da je $i\,$ geometrijska oblika vrednosti ${\sqrt {-1}}\,$.

Enotski bivektorji in usmerjene površine.

Zgodovina

Povezava med geometrijo in algebro sega nazaj v Evklidovo delo Elementi. Geometrijska algebra se ni razvijala vse do leta 1844, ko se je pričelo sistematično opisovati geometrijske značilnosti in transformacije prostora. V tem letu je nemški polihistor Hermann Günther Grassmann (1809–1877) vpeljal geometrijsko algebro. Grassmannov sistem se je lahko uporabil za različne vrste prostorov. V letu 1878 je angleški matematik in filozof William Kingdon Clifford uporabil Grassmannovo algebro skupaj s kvaternioni, ki jih je odkril irski matematik, fizik in astronom William Rowan Hamilton (1805–1865). Clifford je opisoval kvaternione kot posebno obliko transformacij (imenoval jih je rotorje). Grassmannova algebra pa je opisovala določene značilnosti, kot so dolžina, površina in prostornina. Clifford je definiral nov produkt, ki se imenuje geometrijski produkt.

Naslednji velik razvojni korak je v 19. stoletju popolnoma zasenčil geometrijsko analizo: to je bila vektorska analiza, ki so jo razvili ameriški fizik, kemik in matematik Josiah Willard Gibbs (1839–1903) ter angleški matematik in fizik Oliver Heaviside (1850–1925).

V 20. stoletju se je nadaljeval napredek v proučevanju geometrijske algebre z delom nemškega matematika Hermana Weyla (1889–1955) in francoskega matematika Clauda Chevaleya (1909–1984). Danes je najmočnejši zagovornik geometrijske algebre ameriški fizik David Hestenes (rojen 1933).

Zunanje povezave

• Geometrijska algebra na PlanethMath Arhivirano 2010-12-13 na Wayback Machine. (angleško)
• Geometrijska algebra za začetnike Arhivirano 2016-03-04 na Wayback Machine. (angleško)
• Geometrijska algebra in njena uporaba v matematični fiziki (angleško)
• Einsteinove enačbe in Cliffordova algebra (angleško)
• Uvod v geometrijsko algebro (angleško)
• Geometrijska algebra za fizike (angleško)