Airyjev disk

Airyjev disk.

Uklon na režah različnih oblik, levo reže, desno uklonske slike.

Airyjev dísk [éjrijev ~] je optični pojav, ki se kaže v tem, da na mestu, kjer bi optična naprava morala dati sliko točke, dobimo osrednji svetel del, ki ga obdajajo izmenični svetli in temni kolobarji. Takšno sliko točke imenujemo Airyjev disk. Nastane zaradi uklona svetlobe na okrogli odprtini.Pojav je posebno dobro opazen pri opazovanju skozi astronomski daljnogled, kjer zaradi uklona slika zvezde ni točka, ampak dobimo sliko, ki je sestavljena iz osrednjega svetlega dela in dodatnih svetlih krogov. Takšno sliko dobimo tudi v primeru, ko je slika najbolje izostrena in uporabljamo najboljše leče.

Imenuje se po angleškem matematiku in astronomu Georgu Bidellu Airyju (1801 – 1892).

Velikost Airyjevega diska

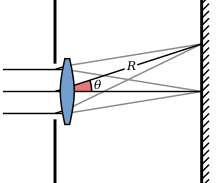
Dovolj daleč od vhodne odprtine, je kot pri katerem nastane prvi minimum v jakosti svetlobe, merjeno v smeri vpadajoče svetlobe, podan z obrazcem:

$\sin \theta \approx 1,22 \frac{\lambda}{d}$

Za majhne kote je to enako

$\theta \approx 1,22 \frac{\lambda}{d}$

V obeh primerih je:

• $\lambda \!$ valovna dolžina svetlobe
• $d \!$ je premer aperture (velikost odprtine pri optični napravi )

Iz tega se vidi, da je Airyjev disk manši, če je apertura večja. To se kaže v tem, da večji teleskopi (z večjo aperturo) dajejo majše slike zvezd.

Zgled

Kot primer vzamimo sliko, ki jo nudi običajna kamera (n. pr. video ali filmska). Kadar padejo Airyjevi diski drug na drugega, ne moremo več ločiti posameznih točk iz slike. Sliki dveh točk še ločimo, če pade prvi maksimum prve točke Airyjevega diska na mesto prvega minimuma druge točke. Ker je kot $\theta \!$ zelo majhen, lahko zapišemo tudi

$\frac{x}{f} = 1,22\ \frac{\lambda}{d}$

kjer je

• $x \!$ razdalja med slikama dveh točk na snemalnem sredstvu (film)
• $f \!$ je razdalja od leče do snemalnega sredstva.

Običajno je snemalno sredstvo oddaljeno od leče za goriščno razdaljo in velja

$x = 1,22\ \frac{\lambda f}{d}$

Intenzivnost svetlobe

Uklon svetlobe na okrogli aperturi. Airyjev disk se lahko opazuje, ko je $R > a^2 / \lambda$.

Uklon na aperturi z lečo. Slika nastane na zaslonu, ki je od leče oddaljen za goriščno razdaljo. Kot opazovanja $\theta$ je enak kot pri sistemu brez leč.

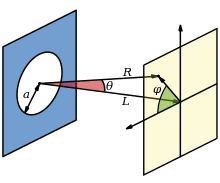
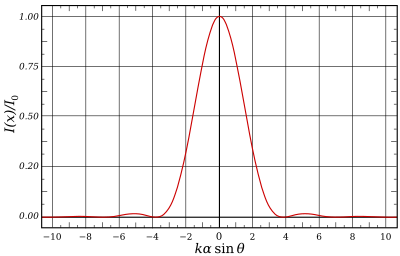
Intenzivnost (energija na enoto površine v časovni enoti, merilo za energijski pretok) svetlobe v odvisnosti od kota je pri okrogli odprtini

$I(\theta) = I_0 \left ( \frac{2 J_1(ka \sin \theta)}{ka \sin \theta} \right )^2 = I_0 \left ( \frac{2 J_1(x)}{x} \right )^2$

kjer je

• $\theta \!$ kot na katerem opazujemo (kot med osjo aperture in smerjo, ki povezuje opazovano točko in središče Airyjevega diska – glej sliko)
• $I_0 \!$ maksimalna intenzivnost Airyjevega diska v središču
• $J_1 \!$ Besslova funkcija prvega reda
• $k= \frac {2\pi} {\lambda} \!$ valovno število
• $a \!$ polmer aperture

Diagram intenzivnosti svetlobe $I(x)/I_0 \!$ v Airyjevem disku.

Skupna moč $P(x)/P_0 \!$ v primerjavi z intenzivnostjo $I(x)/I_0 \!$.

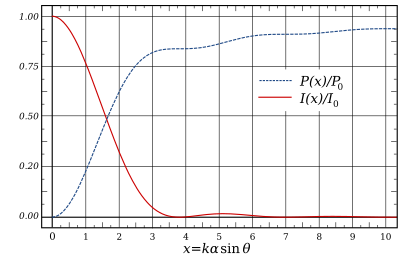Z integracijo izraza za $I(\theta) \!$ dobimo skupno moč, ki se nahaja v Airyjevem disku določene velikosti

$P(\theta) = P_0 [ 1 - J_0^2(ka \sin \theta) - J_1^2(ka \sin \theta) ]$

kjer je

• $J_0$ Besslova funkcija
• $J_1$ Besslova funkcija

Zunanje povezave

• Airyjev disk na Encyclopedia of Science (v angleščini)
• Opis Airyjevega diska (v angleščini)
• Fotografija in uklon (v angleščini)
• Mikroskopija in uklon (v angleščini)
• Uklon na okrogli odprtini (v angleščini)