Radian
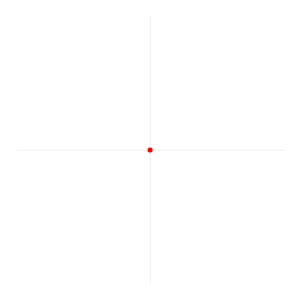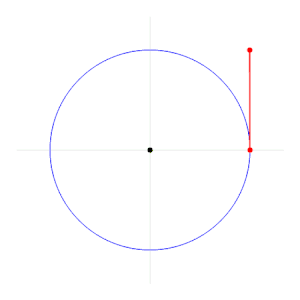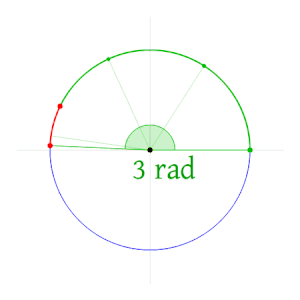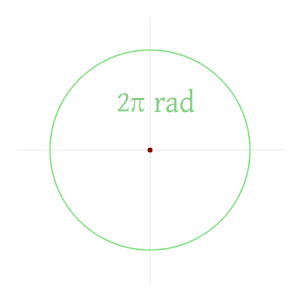
Radián je enota za merjenje ravninskih kotov. Določena je kot razmerje med dolžino krožnega loka, ki ga določa kot, in polmerom.
1 radian, izražen v kotnih stopinjah, je enak:
1 stopinja je torej enaka
Polni kot znaša
Ker je radian razmerje dveh dolžin, je brezrazsežna enota. Zaradi tega ga ne moremo šteti med osnovne enote mednarodnega sistema enot in je zato skupaj s steradianom dopolnilna enota SI.
Ker enota nima razsežnosti, je največkrat ne pišemo ob merskem številu. Velja tudi obratno, če ob merskem številu kota ni podana enota, se predpostavi, da je enota radian.
Ker se iztegnjenih in polnih kotov ne da podati z okroglim celim številom, radian ni najprimernejši za vsakdanjo rabo. Zato pa ravno zaradi tega, ker je določen kot razmerje dolžin, velja v matematiki za »bolj naravno« enoto kot stopinja. Tudi enačbe za izračun kotnih funkcij (npr. Taylorjeva vrsta) veljajo za kote podane v radianih.

![{\displaystyle {\varphi }{\,[\mathrm {rad} ]}={\frac {l}{r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec4f403ab7293523309e3593e8ae55f04bc620ea)


