Talesov izrek

Tálesov izrèk je izrek (imenovan v čast Talesu) v geometriji, ki pravi, da je obodni kot nad premerom krožnice pravi; če imamo torej premer AC neke krožnice in od A in C različno točko B na njenem obodu, je kot ABC pravi kot.

Talesov izrek

Dokaz

Točka O je središče krožnice; ker je OA = OB = OC, sta ΔOAB in ΔOBC enakokraka trikotnika in od tod sledi enakost kotov OBC = OCB in BAO = ABO. Označimo γ = BAO and δ = OBC.

Vsota kotov v trikotniku OAB je 180°

2γ + γ ′ = 180°

in tudi v trikotniku OBC

2δ + δ ′ = 180°

velja pa tudi

γ ′ + δ ′ = 180°

Seštejemo prvi enačbi in odštejemo tretjo ter dobimo:

2γ + γ ′ + 2δ + δ ′ − (γ ′ + δ ′) = 180°

iz česar sledi

γ + δ = 90°

Q.E.D.

Uporaba

Konstrukcija tangente

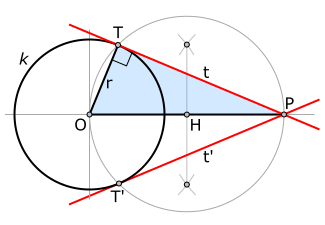
Izrek uporabimo pri konstrukciji tangente na krožnico k, ki gre skozi točko P. Določimo točko H tako da je OH = HP (razpolovišče daljice OP). Krog (H, OH) seka krožnico k v točkah T in T', ki sta dotikališči tangent.

Glej tudi

• izrek o središčnem in obodnem kotu