7-simpleks

pravilni oktaekson (7-simpleks)
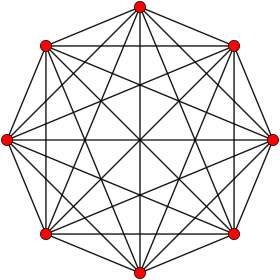
Ortogonalna projekcija v Petriejevem mnogokotniku
vrsta	pravilni 7-politop
družina	simpleks
Schläflijev simbol	{3,3,3,3,3,3}
Coxeter-Dinkinov diagram
6-stranske ploskve	8 6-simpleks
5-stranske ploskve	28 5-simpleks
4-stranske ploskve	56 5-celica
celice	70 tetraeder
stranske ploskve	56 trikotnik
robovi	28
oglišča	8
slika oglišč	6-simpleks
Petriejev mnogokotnik	osemkotnik
Coxeterjeva grupa	A7 [3,3,3,3,3,3]
dualnost	sebidualni
značilnosti	konveksni

7-simpleks (tudi oktaekson ali oktatop) je v 7-razsežni geometriji sebi dualni pravilni 7-politop. Ima 8 oglišč, 28 robov, 56 trikotnih stranskih ploskev, 70 tetraederskih celic, 56 5-celic s 5 stranskimi ploskvami, 28 5-simpleksov s 6 stranskimi ploskvami in 8 6-simpleksov s 7 stranskimi ploskvami. Ima diedrski kot cos⁻¹(1/7)kar je približno 81,79°.

Koordinate oglišč

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)$

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)$

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)$

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)$

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)$

$\left({\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)$

$\left(-{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)$

Sorodni politopi

t0	t1	t2	t3	t0,1	t0,2	t1,2	t0,3
t1,3	t2,3	t0,4	t1,4	t2,4	t0,5	t1,5	t0,6
t0,1,2	t0,1,3	t0,2,3	t1,2,3	t0,1,4	t0,2,4	t1,2,4	t0,3,4
t1,3,4	t2,3,4	t0,1,5	t0,2,5	t1,2,5	t0,3,5	t1,3,5	t0,4,5
t0,1,6	t0,2,6	t0,3,6	t0,1,2,3	t0,1,2,4	t0,1,3,4	t0,2,3,4	t1,2,3,4
t0,1,2,5	t0,1,3,5	t0,2,3,5	t1,2,3,5	t0,1,4,5	t0,2,4,5	t1,2,4,5	t0,3,4,5
t0,1,2,6	t0,1,3,6	t0,2,3,6	t0,1,4,6	t0,2,4,6	t0,1,5,6	t0,1,2,3,4	t0,1,2,3,5
t0,1,2,4,5	t0,1,3,4,5	t0,2,3,4,5	t1,2,3,4,5	t0,1,2,3,6	t0,1,2,4,6	t0,1,3,4,6	t0,2,3,4,6
t0,1,2,5,6	t0,1,3,5,6	t0,1,2,3,4,5	t0,1,2,3,4,6	t0,1,2,3,5,6	t0,1,2,4,5,6	t0,1,2,3,4,5,6

Zunanje povezave

• Politopi različnih razsežnosti (angleško)
• Slovar mnogorazsežnosti (angleško)
• 7-simpleks v Glossary for Hyperspace (angleško)