Nihalo

Nihálo je telo, sposobno nihati. Poznamo več vrst nihal:
- Nihalo na vijačno vzmet ali vzmetno nihalo je drobna utež, obešena na vijačni vzmeti.
- Težno nihalo je utež, obešena na koncu toge ali raztegljive žice ali palice. Če ga dvignemo iz navpičnega položaja, se bo zanihalo nazaj in naprej pod vplivom težnosti okoli svoje središčne (najnižje) točke.
- Nitno ali matematično nihalo ima eno krajišče zelo tanke vrvice z zanemarljivo maso, pritrjeno, na drugem pa je na razdalji l obešeno majhno telo, ki ga obravnavamo kot točkasto telo.
- Torzijsko nihalo je telo, obešeno s tanko žico ali s prožno nitjo, ki zaradi upogibanja žice ali niti krožno koleba.
Splošna enačba nihala[uredi | uredi kodo]
Splošna diferencialna enačba nihala je:
kjer je m masa telesa, l dolžina nihala, = m l2 vztrajnostni moment, kot zasuka od ravnovesne lege, g težni pospešek.
Nihala na vijačno vzmet[uredi | uredi kodo]
Pri nihalu na vijačno vzmet je masa vzmeti s koeficientom k mnogo manjša od mase telesa m. Vzmet deluje na utež s silo F = - k x po Hookovem zakonu. Iz 2. Newtonovega zakona F = m a = - k x sledi nihajni čas:
Krožna frekvenca je:
Težna nihala[uredi | uredi kodo]
Gibanje idealnega nihala lahko za majhne zasuke opišemo matematično kot enostavno harmonično gibanje, saj je sprememba potencialne energije ob vznožju krožnega loka skoraj sorazmerna kvadratu zasuka. Pri resničnih težnih nihalih ni neskončno majhnih zasukov in je njihovo obnašanje dejansko nelinearno. Resnična nihala bodo pri zibanju izgubljala energijo in bo njihovo gibanje dušeno. Velikost nihanja bo pojemala približno eksponentno s časom.
V primeru nihala z maso m, ki niha na osi ζ z razdaljo r* od svojega težišča z vztrajnostnim momentom glede na to os pri gravitacjskem pospešku okolice g je nihajni čas celega nihaja:
Enačba velja le, kadar je zasuk majhen. Popoln opis obnašanja nihala ni matematično preprost.
Za težno nihalo ima diferencialna enačba obliko:
Dve združeni nihali tvorita dvojno nihalo, dve povezani pa sklopljeni nihali. Gibanje dvojnega nihala je kaotično.
Nitna nihala[uredi | uredi kodo]
Posebej enostaven primer težnega nihala je nitno ali matematično nihalo, pri katerem je celotna masa zbrana v točkastem telesu, obešenem na neraztegljivi vrvici, katere maso lahko zanemarimo. Tukaj je r* = l in = m l2, tako da je diferencialna enačba:
imenovana tudi Mathieujeva enačba, ter nihajni čas:
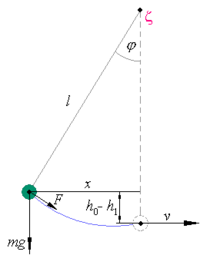
Enačbo lahko dobimo tudi iz načela ohranitve mehanske energije: vsako dano telo, ki pade za navpično razdaljo h, bo imelo kinetično energijo, ki jo je pri padcu pridobilo. Gravitacijska potencialna energija se pri tem spremeni v kinetično.
Sučna nihala[uredi | uredi kodo]
Če je vztrajnostni moment telesa glede na njegovo os nihanja ζ in K torzijski koeficient (ali sučna konstanta) niti (navor, ki je potreben, da se telo zasuče za kot enega radiana), potem je nihajni čas nihanja sučnega nihala:
J in K lahko določimo s poskusom. Merimo nihajni čas in seštejemo prispevek drugega telesa z znanim vztrajnostnim momentom , in dobimo nov nihajni čas nihanja :
Rešimo obe enačbi in dobimo:
Nihajoča nemirka v uri je sučno nihalo, kjer visečo nit zamenjajo tenke vzmeti in čepi. Uro najprej grobo naravnamo s prilagajanjem J. V ta namen služijo vijaki, vstavljeni radialno v okvir nemirke. Še natančneje pa uro naravnamo s spreminjanjem dolžine tenke vzmeti in s tem torzijski koeficient K.
Viri in opombe[uredi | uredi kodo]
Glej tudi[uredi | uredi kodo]
- balistično nihalo, dobrota nihala, dušeno nihanje, fizika, Foucaultovo nihalo, kompenzacijsko nihalo, nedušeno nihanje, sestavljeno nihalo, vsiljeno nihanje, ura na nihalo
- radiestezijsko nihalo