Iz Wikipedije, proste enciklopedije
 Konturni graf funkcije beta
Konturni graf funkcije beta
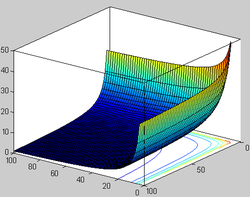 Graf funkcije beta za pozitivne x in y
Graf funkcije beta za pozitivne x in y
Funkcija beta, imenovana tudi Eulerjev integral prve vrste, je v matematiki specialna funkcija dveh argumentov, definirana kot:

Funkcijo beta sta raziskovala Euler in Legendre, ime pa ji je dal Binet.
Funkcija beta je simetrična, kar pomeni da argumenta lahko zamenjata mesti, in velja:

Funkcijo beta se lahko zapiše v različnih oblikah.
Dokazati je mogoče, da se da funkcijo beta izraziti s funkcijo gama:







Druga enakost kaže, da je  .
.
Podobno kot funkcija gama za cela števila opisuje fakultete, lahko funkcija beta določa binomski koeficient s primernimi indeksi:

Funkcija beta je bila prva znana raztrosna amplituda v teoriji strun, kar je prvi domneval Veneziano. Pojavlja se tudi v teoriji procesa prednostne povezanosti, vrste stohastičnega procesa žare.














