Elektromagnetno valovanje
V fiziki se elektromagnetno sevanje (EM sevanje ali EMR) nanaša na valove (ali njihov kvante, fotone) elektromagnetnega polja, ki se širijo (sevajo) skozi prostor-čas in s seboj nosijo elektromagnetno energijo sevanja.[1] Primeri EM sevanja so radijski valovi, mikrovalovi, infrardeča, (vidna) svetloba, ultravijolično sevanje, žarki X in žarki gama.[2]
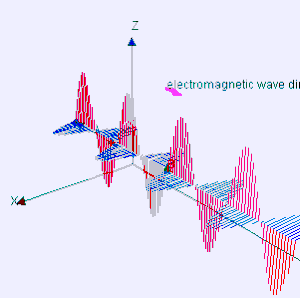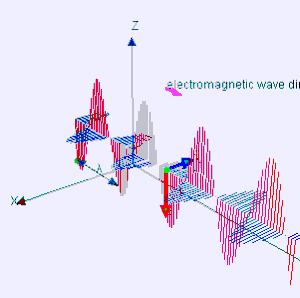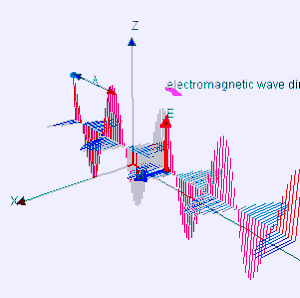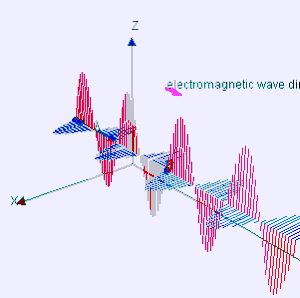
Klasično elektromagnetno sevanje je sinhrono nihanje električnega in magnetnega polja, ki se skozi vakuum širi s hitrostjo svetlobe. Polji nihata pravokotno drugo na drugo in pravokotno na smer širjenja energije in valovanja, oblikujeta torej prečni val. Točkovni viri (npr. svetilo) oddajajo valove v obliki krogle. Z vidika elektromagnetnega spektra je za elektromagnetno sevanje značilna frekvenca ali enakovredno njegova valovna dolžina. Poznani deli elektromagnetnega spektra so, po naraščajoči frekvenci in padajoči valovni dolžini: radijski valovi, mikrovalovi, infrardeče sevanje, vidna svetloba, ultravijolično sevanje, rentgenski žarki in žarki gama.[3]
EM sevanje oddaja sistem električno nabitih delcev, valovi po drugi strani pa lahko kasneje interagira z drugimi nabitimi delci. EM valovi odnašajo energijo, gibalno količino in vrtilno količino iz svojega vira in prenašajo te količine na snovjo , s katero pride v stik. Kvanti elektromagnetnega sevanja se imenujejo fotoni, njih mirovna masa je nič. S temi valovi povezano elektromagnetno sevanje se lahko prosto širi ("seva"), brez nadaljnega vpliva nabojev, katerih gibanje te valove proizvaja, ker so valovi od njih dovolj oddaljeni. Zato se EMR tudi včasih opisuje tudi kot daljno polje. Nasprotje je bližnje polje, ki se nanaša na EM polja v bližini nabojev in toka, ki jih neposredno ustvarja, na primer pri pojavih elektromagnetne indukcije in elektrostatične indukcije.
V domeni klasične elektrodinamike elektromagnetno sevanje izpolnjuje naslednje samoumevne fizikalne zakone. EMR prenaša energijo. Zaradi zakona o ohranitvi energije mora vsak EMR imeti vir električnih nabojev, ki so mu dali njegovo energijo. elektromagnetno sevanje se v vakuumu širi brez izgube energije. Tako mora za pretok energije veljati obratni kvadratni zakon. Tok energije elektromagnetnega vala je opisuje Poyntingov vektor, ki je proporcionalen vektorskemu produktu električnega in magnetnega polja valovanja. Iz obratnega kvadratnega zakona tako sledi, da moč električnega polja in magnetnega polja pada kot 1/R, kjer R označuje razdaljo od vira. Iz energije elektromagnetnega sevanja in zakonov Posebne teorije Relativnosti sledi, da se elektromagnetna polja širijo z omejeno hitrostjo, ki v vakuumu znaša hitrost svetlobe. Matematično so elektromagnetna polja prostorski in časovni odvodi tako imenovanih Lienard-Wiechert 4-potencialov. Pospešek nabitih delcev je tako nujen pogoj za sevanje. Elektromagnetna polja poleg tega izpolnjujejo valovno enačbo. Sevanje vira je tako plod interference polj, nastala s pospeševanjem nabojev v viru sevanja. (Nota bene: pospeševanje nabojev ni zadosten pogoj za sevanje. Vzemimo za primer električni tok v obroču, ki je priključen na baterijo. Obroč sam je pri tem negiben. Zaradi krožne oblike prevodnika pa se električni naboji pospešujejo v smeri proti središču obroča. Sistem je časovno neodvisen, in zaradi tega elektromagnetne energije ne oddaja na okolje. Naboji v sistemu se torej pospešujejo, vendar sistem zaradi destruktivne interference ne seva).
V kvantni teoriji electromagnetizma,[4] elektromagnetno sevanje sestavljajo fotoni, osnovni delci, odgovornni za vse elektromagnetne interakcije.[5] Kvantni učinki so dodatni vir EMR, kot je na primer prehod elektronov na nižjo raven energije v atomarnem sevanju in pri sevanju črnega telesa. Energija fotonov je kvantizirana in je tem večja, tem višja je njih frekvenca. Ta odnos opisuje Planck-Einsteinova relacija E = hv E = hν, kjer E je energija fotona, ν njegova frekvenca, h pa Planckova konstanta. En foton žarka gama na primer, lahko tako nosi ~100.000-krat več energije kot en foton vidne svetlobe.
Učinki EMR na kemijske spojine in biološke organizme so odvisni tako od moči sevanja kot od njegove frekvence. EM sevanja vidnih ali nižjih frekvenc (kot so vidna svetloba, infrardeče sevanje, mikrovalovi in radijski valovi), se imenujejo ne-ionizirajoča sevanja, ker njihovi fotoni posamično nimajo dovolj energije, da ionizirajo atome ali molekule. Učinki te vrste sevanj na kemijske sisteme in živo tkivo so predvsem posledica za segrevanja zaradi prenosa energije mnogih fotonov. V nasprotju s tem imenujemo kratkovalovni UV ionizirajoča sevanja, saj imajo posamezni fotoni s tako visoko frekvenco dovolj energije, da ionizirajo molekule ali prekinejo kemijske vezi. Ta sevanja so sposobna povzročiti kemične reakcije in poškodovati žive celice bolj jih preprosto ogrevanje, tako da so nevarnost za zdravje.
Izraza »elektromagnetno valovanje« in »elektromagnetno sevanje« se pogosto uporabljata kot sopomenki, čeprav, strogo gledano, ne moremo govoriti o sevanju, kadar se valovanje ne razširja po praznem prostoru (npr. v optičnem vlaknu ali koaksialnem kablu).
Fizika[uredi | uredi kodo]
Teorija[uredi | uredi kodo]
Maxwellove enačbe[uredi | uredi kodo]
Maxwell je izpeljal na valovno obliko električnih in magnetnih enačb, in tako odkril in utemeljil valovno naravo električnih in magnetnih polj in njih simetrijo. Ker je bila hitrost valovanja, ki jo napoveduje valovna enačba, enaka izmerjeni hitrosti svetlobe, je Maxwell prišel do zaključka, da je tudi svetloba sama elektromagnetno valovanje.[6][7] Maxwellove enačbe je potrdil Heinrich Hertz s poizkusi z radijskimi valovi.
Po Maxwellovih enačbah je električno polje, katerega jakost je prostorsko odvisna, vedno povezano z magnetnim poljem, ki se s časom spreminja.[8] Prav tako je prostorsko odvisno magnetno polje povezano električnim poljem, ki se časovno spreminja. Valovanje električnega polja vedno spremlja valovanje magnetnega polja in obratno. Pri tem odosu med pojavoma ne gre za vzrok in posledico, do obeh pride skupaj, podobno kot velja za čas in prostor, kjer se spremembe pojavijo skupaj in so med seboj povezane v posebne relativnosti. Dejansko lahko na magnetna polja gledamo kot na relativistično krivljenje električnega polja, tako da je vez s spremembami v prostoru in času več kot samo analogija. Obe polji skupaj predstavljata premikajoči se elektromagnetni val, ki se širi v prostor in ne potrebuje več stika s svojim izvorom. Oddaljeno EM polje, ki ga je vir ustvaril, nosi s seboj energijo, ki »seva« skozi prostor, od tod tudi izraz »sevanje«.
Delčnovalovna dualnost[uredi | uredi kodo]
Moderna teoretična razlaga svetlobe sloni na dejstvu, da jo je mogoče razumeti hkrati kot valovanje in kot delce. Tako je treba razumeti ne samo svetlobo, temveč vse, kar se lahko s preskusi zazna. Vidik delcev je laže prepoznati, oziroma je bolj neposreden, kadar gre za predmete z veliko maso. Drzna trditev, ki jo je leta 1924 objavil Louis de Broglie, je vodila do preskusov, ki so potrdili dualnost elektrona.[9]
Bližnja in daljna polja[uredi | uredi kodo]

Pri elektromagnetnem sevanju (npr. pri mikrovalovih, ki jih oddaja antena zgoraj) se izraz se nanaša le na del elektromagnetnega polja , ki seva v neskončni prostor (točneje, prostor, katerega mere so občutno višje kot je pa valovna dolžina sevanja) in katerega moč pada, kot predvideva obratni kvadratni zakon moči, tako da je skupna izsevana energija, ki jo oddaja namišljena krogelna površina vedno enaka, ne glede na to, kako velika je namišljena krogla. En del elektromagnetnega sevanja torej predstavlja daljno polje okoli oddajnika. Tako imenovano "bližnje polje" je mogoče zaznativ bližini oddajnika, gre za del spreminjajočega se elektromagnetnega polja, vendar se ne šteje za elektromagnetno sevanje Maxwellove enačbe so pokazale, da nekateri naboji in tokovi ("viri") ustvarjajo lokalno vrsto elektromagnetnega polja v svoji bližini, da se ne vede kot EMR. Tokovi neposredno proizvajajo magnetno polje, vendar gre pri tem za magnetne dipole, ki imajo omejen doseg. Na podoben način električni naboji, ki jih spreminjajoči se električni potencial (npr. v anteni) med sabo ločuje, ustvarjajo električni dipole, katerih električno polje in s tem vpliv ravno tako pada z razdaljo. Ta polja so bližnje polje v okolici vira EMR. Od teh načinov vedenja ni nobeden odgovoren za EM sevanje. Namesto sevanja povzročajo v elektromagnetnem polju razmere, v katerih se energija učinkovito prenaša le na prejemnike, ki so zelo blizu vira, kot na primer pri magnetni indukciji znotraj transformatorja, ali v povratnem obnašanju pri tuljavi v detektorju kovin. Običajno imajo bližnja polja močan učinek na same vire, ker povzročajo večjo "obremenitev" (nižjo električno reaktivnost) v izvoru ali pri oddajniku , kadarkoli prejemnik iz EM polja črpa energijo. Po drugi strani se ta polja ne "širijo" prosto v prostor in energije ne odnašajo brez omejitve razdalje, temveč prej nihajo in energijo vračajo v oddajnik, če je sprejemnik ne sprejme.
Nasprotje temu je daljno EM polje, ki ga sestavlja sevanje , ki je brez oddajnika v smislu, da (za razliko od primera z električnim transformatorjem) oddajnik potrebuje za posredovanje teh sprememb v okolje moč, ne glede ali se poslani signal prejme takoj ali ne. Ta oddaljeni del elektromagnetnega polja je "elektromagnetno sevanje" (imenovan tudi daljno polje). Daljna polja se širijo (oddajajo), na da pri tem njih vir lahko vplival nanje. To sevanje je tako samostojno in neodvisno v smislu, da sta njegov obstoj in njegova energija, potem ko je zapustilo oddajnik, popolnoma neodvisna tako od oddajnika kot od sprejemnika. Količina energije, ki gre skozi površino okrog vira opisane krogle, se zaradi ohranitve energije ne spreminja. Ker je površina sorazmerna s kvadratom oddaljenosti od vira, gostota moči EM sevanja vedno pada sorazmerno z obratnim kvadratom razdalje od vira; (tako imenovani obratni kvadratni zakon). Pri dipolih blizu vira (bližnje polje) je to drugače, moč pada sorazmerno inverzno tretji potenci razdalje,tako da do prenosa energije ne pride, namesto tega "na dolgo roko" zamre, energija pa se (kot rečeno) hitro se vrne v oddajnik, če je sprejemnik (na primer sekundarno navitje v transformatorju) ne absorbira.
Mehanizmi za nastanek daljnega polja so drugačni kot pri bližnjem polju, gre druge postavke v Maxwellovih enačbah. Magnetni del v bližnjem polju je posledica tokov v viru, magnetno polje v EMR pa samo zaradi lokalne spremembe električnega polja. Podobno je električno polje v bližnjem polju neposredna posledica nabojev in njih ločevanja v viru, je v elektromagnetnem sevanju električno polje samo in edino posledica spremembe v lokalnem magnetnem polju. Procesi, po katerih pride do električnih in magnetnih polj, imajo drugačno odvisnost od razdalje, kot pa to velja za dipole pri električne in magnetne dipole pri bližnjih poljih. Iz tega razloga EM sevanje prevladuje po moči "daleč" od vira.
Model delcev in kvantna teorija[uredi | uredi kodo]
Konec 19. stoletja se je znanost morala spopasti z anomalijo, katere jedro je bilo protislovje med valovno teorijo svetlobe in meritvami elektromagnetnega spektra, ki ga oddajajo tako imenovana črna telesa. Fiziki so se s tem problemom, ki se je kasneje postal znan kot ultravijolična katastrofa, brez uspeha borili leta dolgo. Leta 1900 je Max Planck razvil novo teorijo za sevanje črnega telesa , ki je pojasnila izmerjeno obliko spektra. Planck je teorijo utemeljil na ideji, da črna telesa oddajajo svetlobo (in drugih elektromagnetno sevanje) izključno samo v obliki diskretnih svežnjev ali paketov energije, tako imenovanih kvantov. Kasneje je Albert Einstein prišel do zaključka, da je svetlobne kvante treba razumeti kot delce. Kasneje so jih poimenovali foton, v skladu z imenovanjem drugih tedaj poznanih elementarnih delcev, kot sta elektron in proton. Foton ima energijo E, ki je sorazmerna z njegovo frekvenco, f:
kjer je h je Planckova konstanta, je valovna dolžina in c hitrost svetlobe. Enačba je znana pod imenom Planck–Einsteinova enačba.[10] V kvantni teoriji (glej prvo kvantizacijo) je tako energija fotonov neposredno sorazmerna s frekvenco elektromagnetnega vala.[11]
Tudi gibalna količina fotona p je sorazmerna z njegovo frekvenco in obratno sorazmerna z njegovo valovno dolžino:
Povod za Einsteinov predlog, da svetlobo sestavljajo delci (oziroma da v nekaterih okoliščinah deluje kot delci) je bil poizkus, katerega rezultat valovna teorija ni bila sposobna pojasniti: v fotoelektričnem pojavu svetloba, ki pada na kovinsko površino, izbija elektrone iz površine. Energija posameznih elektronov je pri tem sorazmerna frekvenci, ne pa jakosti svetlobe. Poleg tega pod določeno minimalno frekvenco, ki je odvisna od uporabljene kovine, ne pride do izstopanja elektronov, ne glede na jakost svetlobe. Te ugotovitve so v nasprotju z valovno teorijo leta dolgo so fiziki poskušali zaman najti razlago za to. Leta 1905 je Einstein predlagal rešitev za to uganko z alternativnim pogledom na EMR kot na tok fotonov. Znanstvena javnost je bila dolgo časa skeptična, Tako da je Einstein dobil za razlago fotoelektričnega pojava Nobelovo nagrado šele leta 1921.
Hitrost svetlobe[uredi | uredi kodo]
Ko prevodnik (žica ali pa na primer antena) prevaja izmenični tok, oddaja elektromagnetno sevanje s frekvenco, ki je enaka frekvenci električnega toka. V številnih primerih je mogoče identificirati električni dipolni moment, ki nastane zaradi ločevanja nabojev pod vplivom električnega potenciala. Premikanje nabojev povzroči osciliranje dipola in spreminjajoča se električno in magnetno polje in s tem elektromagnetno sevanje.Na kvantni ravni pride do sevanja, ko delec z nabojem kot valovni paket oscilira oziroma se premika. Nabiti delci se v stacionarnem stanju ne premikajo, vendar lahko pri superpoziciji teh stanj pride do prehodnega stanja z električnim dipolnim momentom, ki oscilira. Posledica je preskok iz enega v drugo kvantno stanje, ki ga spremlja sevanje. Primer za to so atomi, ki ob prehodu iz enega stacionarnega stanja v drugo sevajo fotone.
Z valovnega vidika svetlobo opisuje njena hitrost (svetlobna hitrost), valovna dolžina in frekvenca. Z vidika delcev predstavlja svetloba tok fotonov. Njih energija je povezana z njih frekvenco po Planckovi enačbi E = hf, kjer je E energija fotona, h = 6.626 × 10−34 J·s je Planckova konstanta in f je frekvenca vala.En zakon velja v vsakem primeru: elektromagnetno valovanje se v vakuumu, z vidika opazovalca, širi s svetlobno hitrostjo, neodvisno od hitrosti, s katero se opazovalec giba - osnova Einsteinove posebne teorije relativnosti. V sredstvih (ki niso vakuum) je potrebno upoštevati lomni indeks snovi, to je količnik med hitrostjo v vakuumu in hitrostjo v snovi.
Posebna teorija relativnosti[uredi | uredi kodo]
Konec devetnajstega stoletja so odkrili različne eksperimentalne anomalije, ki jih s preprosto valovno teorijo ni bilo mogoče razložiti. Ena od teh anomalij se je tikala spora glede hitrosti svetlobe. Hitrost svetlobe in drugih elektromagnetnih sevanj, kot so jo predvidevale Maxwellove enačbe, ni bila mogoča, razen če se enačb ni prilagodilo tako, kot sta ga najprej predlagala FitzGerald in Lorentz (glej zgodovino posebne relativnosti), saj bi v nasprotnem primeru hitrost bila odvisna od hitrosti opazovalca glede na "medij" (tako imenovani svetlobni eter), ki naj bi "prenašal" elektromagnetne valove, podobno kot zrak prenaša zvočne valove. Poskusi niso ugotovili nobenega vpliva hitrosti, s katero se vir valovanja in opazovalec premikata relativno drug na drugega. Leta 1905 je Einstein predlagal, da je prostor in čas in s tem tudi vse druge procese in zakone kot pojme, ki so odvisni od hitrosti. Spremenjeno pojmovanje prostora in časa je pogoj za konstantno hitrost svetlobe in vseh elektromagnetnih sevanj z vidika opazovalca - tudi opazovalca, ki ne miruje, temveč se premika.
Elektromagnetni spekter[uredi | uredi kodo]

Elektromagnetno sevanje (poimenovanje »sevanje« izključuje pojave statično elektriko in magnetno ter bližnje polje) je razvrščen glede na valovno dolžino na radiu, mikrovalovnih, infrardečo, vidno, uv, X-žarke in gama žarke. Samovoljno elektromagnetni valovi, ki se lahko izrazi z Fouriereve analizo v smislu sinusiodalen dvobarvni valovi, ki pa se lahko vsak, ki se delijo v teh regijah EMR spektra.
X-žarki in gama žarki[uredi | uredi kodo]
Elektromagnetno sevanje, ki ga sestavljajo fotoni, ki imajo minimalne-ionizacija energije, ali več, (ki zajema celoten spekter s krajše valovne dolžine), je zato imenovan ionizirajočega sevanja. (Številne druge vrste ionizirajočega sevanja so narejene iz ne-EM delci). Elektromagnetna-vrste ionizirajočega sevanja razteza od ekstremno ultravijolično za vse višjih frekvencah in krajše valovne dolžine, kar pomeni, da vse X-žarke in gama žarke, ki izpolnjujejo pogoje. Ti so sposobni najbolj hudo vrsta molekulske poškodbe, ki se lahko zgodi v biologije za vse vrste bioloških molekul, vključno z mutacijo in raka, in pogosto na velikih globin pod kožo, ker je zgornji konec X-ray spektra, in vse gamma ray spektra, prodre skozi snovi.
Atmosfera in magnetosfera[uredi | uredi kodo]

Večino ultravioletnih žarkov in žarkov X zadrži najprej absorpcija v molekularnem dušiku, nato pa (za valovne dolžine v zgornji UV) z elektronska ekscitacija di-kisika in končno ozona za srednji pas UV. Le 30% sončne ultravijolične svetlobe doseže tla.
Vidna svetloba se dobro prenaša skozi zrak, ker nima dovolj energije, da bi vzbudila dušik, kisik, ali ozon, po drugi strani pa ima preveč energije za vzbujanje vibracij v molekulah vodne pare.[navedi vir] Absorpcijski pasovi v infrardečem področju so posledica vibracijskih ekscitacij v vodni pari. Pri še nižjih energijah, to je pod pragom za vodno paro, ozračje postane znova prozorno, tako da je mogoče brez izgub skozi atmosfero prenašati mikrovalove in radijske valove.
Sklici[uredi | uredi kodo]
- ↑ Purcell, Edward M.; Morin, David J. (2013). Electricity and Magnetism (3. izd.). New York: Cambridge University Press. str. 820. ISBN 978-1-107-01402-2.
str. 430: »These waves... require no medium to support their propagation. Traveling electromagnetic waves carry energy, and... the Poynting vector describes the energy flow...;« str. 440: »... the electromagnetic wave must have the following properties: 1) The field pattern travels with speed c (speed of light); 2) At every point within the wave... the electric field strength E equals »c« times the magnetic field strength B; 3) The electric field and the magnetic field are perpendicular to one another and to the direction of travel, or propagation.«
- ↑ Browne, Michael (2013). Physics for Engineering and Science (2. izd.). New York: McGraw Hill/Schaum. str. 319–320. ISBN 978-0-07-161399-6.
str. 319: »For historical reasons, different portions of the EM spectrum are given different names, although they are all the same kind of thing. Visible light constitutes a narrow range of the spectrum, from wavelengths of about 400-800 nm....«; str. 320: »An electromagnetic wave carries forward momentum... If the radiation is absorbed by a surface, the momentum drops to zero and a force is exerted on the surface... Thus the radiation pressure of an electromagnetic wave is (formula).«
- ↑ Maxwell, J. Clerk (1865). »A Dynamical Theory of the Electromagnetic Field«. Philosophical Transactions of the Royal Society of London. Zv. 155. str. 459–512. doi:10.1098/rstl.1865.0008.
- ↑ »Electromagnetic Spectrum facts, information, pictures | Encyclopedia.com articles about Electromagnetic Spectrum«. www.encyclopedia.com (v angleščini). Arhivirano iz spletišča dne 13. junija 2017. Pridobljeno 4. septembra 2017.
- ↑ »The Dual Nature of Light as Reflected in the Nobel Archives«. www.nobelprize.org. Arhivirano iz spletišča dne 15. julija 2017. Pridobljeno 4. septembra 2017.
- ↑ »Electromagnetic radiation - New World Encyclopedia«. New World Encyclopedia (v angleščini). Arhivirano iz spletišča dne 3. julija 2017. Pridobljeno 4. septembra 2017.
- ↑ »The Impact of James Clerk Maxwell's Work«. James Clerk Maxwell Foundation. Arhivirano iz spletišča dne 17. septembra 2017. Pridobljeno 4. septembra 2017.
- ↑ Purcell, str. 438, section 9.4: An Electromagnetic Wave.
- ↑ Browne, Michael (2010). »de Broglie Waves«. Physics for Engineering and Science (2. izd.). McGraw-Hill/Schaum. str. 382. ISBN 978-0-07-161399-6.
Svetloba ima lastnosti valov (interferenca, lom) in lastnosti delcev (fotoelektrični učinek, sipanje.
- ↑ Paul M. S. Monk (2004). Physical Chemistry. John Wiley and Sons. str. 435. ISBN 978-0-471-49180-4.
- ↑ Weinberg, S. (1995). The Quantum Theory of Fields. Zv. 1. Cambridge University Press. str. 15–17. ISBN 0-521-55001-7.



