Regularni graf

Regularni graf je v teoriji grafov graf brez zank in večkratnih povezav v katerem ima vsaka točka enako število sosednjih točk, oziroma vsaka točka ima enako stopnjo ali valenco. Za regularni usmerjeni graf mora veljati tudi strožji pogoj, da je stopnja vstopajočih povezav enaka stopnji odtekajočih povezav.^[1] Regularni graf s točkami stopnje k se imenuje regularni graf stopnje k ali k-regularni graf.

Osnovne značilnosti[uredi | uredi kodo]

Regularne grafe stopnje vsaj 2 je lahko razvrstiti: 0-regularni graf vsebuje nepovezane točke, 1-regularni graf vsebuje nepovezane povezave, 2-regularni graf pa vsebuje nepovezane cikle.

3-regularni graf je znan kot kubični graf, 4-regularni graf pa kot kvartični graf.

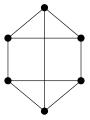
Krepkoregularni graf je regularni graf kjer ima vsak sosednji par točk enako število skupnih sosednjih točk l, in vsak nesosednji par točk enako število skupnih sosednjih točk n. Najmanjša grafa, ki sta regularna, ne pa tudi krepkoregularna, sta cikel in cirkulantni graf na 6-tih točkah.

Polni graf $K_{m}$ je krepkoregularen za vsak $m$ .

Nash-Williamsov izrek pravi, da ima vsak k-regularni graf na $2k+1$ točkah Hamiltonov cikel.

0-regularni graf
1-regularni graf
2-regularni graf
3-regularni graf (kubični graf)

Polni graf K₅
graf 5-celice, najmanjši možni 4-regularni graf (kvartični graf)
Oktaedrski graf
(graf trikotniške antiprizme). Edini kvartični graf na 6-ih točkah.
Cirkulantni graf $C_{7}(1,2)\,$
Cirkulantni graf $C_{7}(1,3)\,$
Kvartični graf na 7-ih točkah

Pogoja za obstoj[uredi | uredi kodo]

Dobro je znano, da sta potrebna in zadostna pogoja za obstoj $k$ -regularnega grafa reda $n$ , da velja $n\geq k+1$ in, da je produkt $nk$ sod. Tedaj je lahko skonstruirati regularne grafe z upoštevanjem ustreznih parametrov cirkulantnih grafov.

Algebrske značilnosti[uredi | uredi kodo]

Naj je A matrika sosednosti grafa. Potem je graf regularen, če in samo če je ${\textbf {j}}=(1,\dots ,1)$ lastni vektor A.^[2] Njegova [flastna vrednost]] bo konstantna stopnja grafa. Lastni vektorji, ki odgovarjajo drugim lastnim vrednostim, so pravokotni na ${\textbf {j}}$ , tako da za vsak tak lastni vektor $v=(v_{1},\dots ,v_{n})$ velja $\sum _{i=1}^{n}v_{i}=0$ .

Regularni graf stopnje k je povezan, če in samo če ima lastna vrednost k multiplikativnost ena. Pogoj je posledica Perron-Frobeniusovega izreka.^[2]

Obstaja tudi kriterij za regularne in povezane grafe: graf je povezan in regularen, če in samo če je matrika enic J, kjer je $J_{ij}=1$ , algebra sosednosti grafa, kar pomeni, da je linearna kombinacija potenc A.^[3]

Naj je G k-regularni graf s premerom D in lastnimi vrednostmi matrike sosednosti $k=\lambda _{0}>\lambda _{1}\geq \cdots \geq \lambda _{n-1}$ . Če G ni dvodelen, velja:

D\leq {\frac {\log {(n-1)}}{\log(\lambda _{0}/\lambda _{1})}}+1.

^[4]

Število neizomorfnih regularnih grafov[uredi | uredi kodo]

Število možnih neizomorfnih povezanih k-regularnih grafov na n točkah podaja naslednja razpredelnica:

n	3	4	5	6	7	8	9	10	11	12
	A002851	A006820	A006821	A006822	A014377	A014378	A014381	A014382	A014384
0	1	1	1	1	1	1	1	1	1	1
1	0	0	0	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0
4	1	0	0	0	0	0	0	0	0	0
5	0	1	0	0	0	0	0	0	0	0
6	2	1	1	0	0	0	0	0	0	0
7	0	2	0	1	0	0	0	0	0	0
8	5	6	3	1	1	0	0	0	0	0
9	0	16	0	4	0	1	0	0	0	0
10	19	59	60	21	5	1	1	0	0	0
11	0	265	0	266	0	6	0	1	0	0
12	85	1544	7848	7849	1547	94	9	1	1	0
13	0	10778	0	367860	0	10786	0	10	0	1
14	509	88168	3459383	21609300	21609301	3459386	88193	540	13	1
15	0	805491	0	1470293675	0	1470293676	0	805579	0	17
16	4060	8037418	2585136675	113314233808	733351105934	733351105935	113314233813	2585136741	8037796	4207
17	0	86221634	0	9799685588936	0		0	9799685588961	0	86223660
18	41301	985870522	2807105250897
19	0	11946487647	0		0		0		0
20	5104891	152808063181
21	0	2056692014474	0		0		0		0
22	7319447	28566273166527

Ustvarjanje regularnih grafov[uredi | uredi kodo]

Regularni grafi se lahko ustvarjajo s programom GenReg.^[5]

Glej tudi[uredi | uredi kodo]

Sklici[uredi | uredi kodo]

↑ Chen (1997), str. 29.
↑ ^2,0 ^2,1 Cvetković; Doob; Sachs (1998).
↑ Curtin (2005).
↑ Quenell (1992).
↑ Meringer (1999).

Viri[uredi | uredi kodo]

Chen, Wai-Kai (1997), Graph Theory and its Engineering Applications, World Scientific, ISBN 978-981-02-1859-1
Curtin, Brian (2005), »Algebraic characterizations of graph regularity conditions«, Designs, Codes and Cryptography, 34 (2–3): 241–248, doi:10.1007/s10623-004-4857-4, MR 2128333
Cvetković, Dragoš M.; Doob, M.; Sachs, H. (1998), Spectra of Graphs: Theory and Applications (3. rd rev. enl. izd.), New York: Wiley
Meringer, Markus (1999), »Fast generation of regular graphs and construction of cages« (PDF), Journal of Graph Theory, 30 (2): 137–146, doi:10.1002/(SICI)1097-0118(199902)30:2<>1.0.CO;2-G
Quenell, Gregory (1992), Spectral diameter estimates for k-regular graphs (PDF) (v angleščini), arhivirano iz prvotnega spletišča (PDF) dne 6. januarja 2014, pridobljeno 29. junija 2016

Zunanje povezave[uredi | uredi kodo]

Weisstein, Eric Wolfgang. »Regular Graph«. MathWorld.
Weisstein, Eric Wolfgang. »Strongly Regular Graph«. MathWorld.
GenReg – program in podatki, Meringer, Markus (angleško)
Nash-Williams, Crispin (1969), »Valency Sequences which force graphs to have Hamiltonian Circuits«, University of Waterloo Research Report (v angleščini), Waterloo, Ontario: University of Waterloo

[1] Chen (1997), str. 29.

[Cvetkovic-2] 2,0 ^2,1 Cvetković; Doob; Sachs (1998).

[3] Curtin (2005).

[personal.plattsburgh.edu-4] Quenell (1992).

[5] Meringer (1999).

[1]

[2]

[3]

[4]

[5]