Geometrijska optika
Geometríjska óptika je področje optike, ki svetlobo obravnava kot žarke. Temelji na Fermatovem načelu, ki pravi, da svetloba v poljubnem sredstvu med dvema točkama potuje po najkrajši poti oziroma po poti, za katero porabi najmanj časa. Geometrijska optika ne upošteva valovne narave svetlobe, zato nekaterih svetlobnih pojavov, kot sta uklon in interferenca svetlobe, ne pojasni. Približek geometrijske optike je dober, kadar je valovna dolžina svetlobe mnogo manjša od elementov, skozi katere svetloba potuje. Geometrijska optika predstavlja osnovo za razumevanje delovanja optičnih naprav, kot sta daljnogled in mikroskop. V geometrijski optiki - tako kot v valovni optiki - veljata lomni in odbojni zakon.
V praksi se pogosto uporablja obosni približek geometrijske optike, saj postanejo v tem primeru enačbe, ki opisujejo potovanje žarka, linearne in njihova obravnava enostavnejša.
Obosni približek[uredi | uredi kodo]
Obosni približek obravnava le žarke, ki potujejo pod majhnimi koti glede na optično os. Za majhne kote se lahko kotne funkcije razvije v Taylorjevo vrsto in se obdrži le prvi člen te vrste. Tako velja:
in
pri čemer je kot izražen v radianih.
Enačbe, ki bi sicer vsebovale kotne funkcije, so tako linearne.
Pomembna parametra, s katerima se računa v obosnem približku, sta kot žarka in oddaljenost žarka od optične osi . Ker so enačbe linearne, se lahko celoten račun zapiše z matrikami. Vsakemu optičnemu elementu v optičnemu sistemu, skozi katerega žarek potuje, pripada svoja matrika. Lega in kot žarka po izhodu iz optičnega sistema se tako dobi z navadnim matričnim množenjem. Matrike, ki opišejo prehod žarka skozi optični element, se imenujejo matrike ABCD.
Matrike ABCD[uredi | uredi kodo]
ABCD matrike povezujejo lego in kot žarka tik pred optičnim elementom ter lego in kot žarka tik za optičnim elementom.
Naj bodo oddaljenost žarka od optične osi (lega), kot žarka tik pred optičnim elementom, in pa lega in kot žarka tik za optičnim elementom. Lego in kot žarka pred in po optičnem elementu povezuje matrika ABCD:
Matrika ABCD je različna za različne optične elemente.
Matrike ABCD nekaterih optičnih elementov[uredi | uredi kodo]
| optični element | matrika ABCD | pojasnila |
|---|---|---|
| prazen prostor ali homogena snov s konstantnim lomnim količnikom | d = debelina praznega prostora ali snovi | |
| lom na ravni površini med dvema snovema z različnima lomnima količnikoma | n1 = lomni količnik snovi v legi x1 n2 = lomni količnik snovi v legi x2. | |
| lom na ukrivljeni površini med dvema snovi z različnima lomnima količnikoma | R = krivinski radij površine, R > 0 za konveksno ukrivljeno površino n1 = lomni količnik snovi v legi x1 | |
| odboj na ravnem zrcalu | velja za zrcala, pravokotna na optično os | |
| odboj na ukrivljenem zrcalu | R = krivinski radij zrcala, R > 0 za konkavno zrcalo | |
| tanka leča | f = goriščna razdalja leče, f > 0 za konveksno lečo.
Tanka leča pomeni, da je goriščna razdalja leče mnogo večja od njene debeline. |
Preslikava s tanko lečo[uredi | uredi kodo]
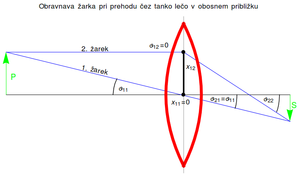
Pri računanju prehoda žarkov skozi tanko lečo je ugodno izbrati dva žarka. Prvi je vzporeden z optično osjo, drugi pa seka optično os ravno ob prehodu skozi lečo. Kjer se žarka sekata, nastane ostra slika predmeta. Vsak žarek se opiše z njegovim odmikom od optične osi () in s kotom (), pod katerim se giblje glede na optično os. Pred vstopom v lečo se žarku, ki je vzporeden z optično osjo, pripiše kot in odmik . Žarku, ki seka optično os ravno ob prehodu čez lečo, pa se pripiše kot in lega . Žarek se preslika s pomočjo matrike ABCD za tanko lečo. Lega in kot žarkov tik za lečo se izračuna tako z enačbo ():
Odboj na zrcalu[uredi | uredi kodo]
Za obravnavo odboja na zrcalu se, podobno kot pri leči, izbere en žarek, ki je vzporeden z optično osjo, in žarek, ki zadane zrcalo ravno na mestu, kjer seka optično os (slika). Kot in lego žarka tik po odboju se izračuna kot:

Kombiniranje matrik ABCD[uredi | uredi kodo]
Matrika ABCD bolj zapletenega optičnega sistema je zmnožek matrik za posamezne optične elemente. Naj se za primer vzame pot žarka iz sredstva z lomnim količnikom skozi sredstvo debeline d z lomnim količnikom .
Takšen optični element se lahko razstavi na tri ločene optične elemente. Najprej žarek potuje skozi ravno mejo med dvema sredstvoma z različnima lomnima količnikoma. Matrika ABCD za ta prehod je:
Nato potuje skozi sredstvo debeline d s konstantnim lomnim količnikom . Matrika ABCD za ta del je:
Nazadnje preide skozi ravno mejo med sredstvoma. Tokrat je treba biti pozoren na to, da žarek pride iz sredstva z lomnim količnikom v sredstvo z lomnim količnikom . Zato je element D v pripadajoči matriki ABCD obrnjen:
Matrika za celotni optični element je matrični produkt gornjih matrik. Pozoren je treba biti na pravilen vrstni red delovanja matrik.
Lomni in odbojni zakon z matrikami ABCD[uredi | uredi kodo]
Na primeru ravne meje med dvema sredstvoma z različnima lomnima količnikoma in na primeru ravnega zrcala se pokaže, da se z matrikami ABCD res dobi lomni in odbojni zakon.
Lom na meji dveh sredstev.[uredi | uredi kodo]
Matrika ABCD, ki ustreza temu prehodu, je:
Z in se označi lega in kot vpadnega žarka glede na optično os, z in pa lega in kot lomljenega žarka glede na optično os. Velja:
Iz zgornje matrične enačbe sledi:
in:
oziroma:
kar pa je ravno lomni zakon, saj je račun narejen v obosnem približku in:
ter:
Odboj na ravnem zrcalu.[uredi | uredi kodo]
Matrika, ki ustreza ravnemu zrcalu, je:
Enačba, ki povezuje lego in kot žarka pred in po odboju, je tako:
Od tu se hitro vidi, da res velja odbojni zakon, saj je:
in:
Viri[uredi | uredi kodo]
- Strnad, Janez (2005). Fizika. Del 2, Elektrika, optika (6. natis izd.). Ljubljana: DMFA-založništvo.
- Zwitter, Tomaž (2002). Naše in druga osončja. [Online] (PDF). Pridobljeno 10. maja 2015.






































