Folkmanov graf

Folkmanov graf
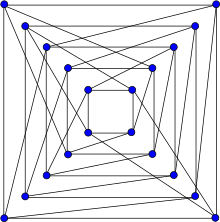Folkmanov graf
Ime	Jon Folkman
Točke	20
Povezave	40
Polmer	3
Premer	4
Notranji obseg	4
Kromatično število	2
Kromatični indeks	4
Značilnosti	regularen dvodelen polsimetričen Eulerjev Hamiltonov popoln

Folkmanov graf je v teoriji grafov neusmerjeni dvodelni regularni graf stopnje 4 z 20 točkami in 40 povezavami. Imenuje se po Jonu Folkmanu.

Folkmanov graf je Hamiltonov graf in ima kromatično število 2, kromatični indeks 4, premer 4, polmer 3 in notranji obseg 4. Je tudi 4-povezan in 4-povezavno-povezan popolni graf.

Algebrske značilnosti

Folkmanov graf je točkovno-prehoden, ne pa tudi povezavno. Je najmanjši neusmerjeni graf, ki je točkovno-prehoden in regularen, ne pa tudi poezavno-prehoden. Takšni grafi se imenujejo polsimetrični grafi. Prvi jih je raziskoval Folkman leta 1967 in odkril graf z 20 točkami, sedaj imenovan po njem.

Kot polsimetrični graf je Folkamnov graf dvodelni graf in ima avtomorfizme za vsak par točk, ne pa za povezave. V spodnji upodobitvi grafa, ki kaže njegovo kromatično število, zelene točke ne moremo preslikati v rdeče z nobenim avtomorfizmom. Lahko pa preslikamo katerokoli rdečo točko v drugo rdečo točko, ter enako tudi zelene točke.

Folkmanov graf ima 8 različnih posplošenih zapisov LCF, tri z eksponentom 5 in pet z eksponentom 1.

Karakteristični polinom Folkmanovega grafa je:

$(x-4) x^{10} (x+4) (x^{2}-6)^{4} \!\, .$

Upodobitve

• 

  Kromatično število Folkmanovega grafa je 2.

• 

  Kromatični indeks Folkmanovega grafa je 4.

• 

  Folkmanov graf je Hamiltonov graf.

Viri

• Folkman, Jon (1967). "Regular line-symmetric graphs". J. Combin. Th. 3: 215–232. doi:10.1016/S0021-9800(67)80069-3. 
• Skiena, S. (1990). Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley. 

Zunanje povezave

• Folkman Graph na MathWolrd (v angleščini)