Linearna enačba
Lineárna enáčba je v matematiki algebrska enačba, v kateri je vsak člen ali konstanta ali produkt konstant s prvo potenco spremenljivke. Enakovredno enačbo dobimo, če enačimo polinom prve stopnje z nič. Enačbe se imenujejo linearne, ker predstavljajo premice v kartezičnem koordinatnem sistemu. Zgled linearne enačbe:
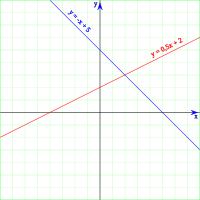
Običajno zapišemo linearno enačbo dveh spremenljivk x in y kot:
V tej obliki konstanta k določa smer premice, konstantni člen n pa določa točko kjer premica seka ordinatno os. Enačbe, ki imajo na primer člene , ali , so nelinearne. Zgled enačbe, ki ni linearna :






