Krivočrtni koordinatni sistem

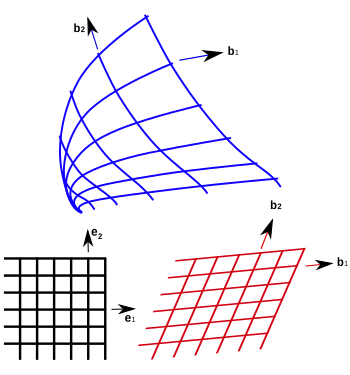
Krivočrtne, afine in kartezične koordinate v dvorazsežnem prostoru.

Krivočrtni koordinatni sistem je koordinatni sistem v Evklidskem prostoru v katerem so lahko koordinatne premice ukrivljene. Te koordinate se lahko dobijo iz kartezičnega koordinatnega sistema z uporabo preslikave, ki je lokalno inverzibilna v vsaki točki. To pa pomeni, da lahko v vsaki točki, ki je dana v kartezičnem koordinatnem sistemu pretvorimo koordinate v krivočrtne in nazaj.

Izraz je skoval francoski matematik Gabriel Lamé (1795 - 1870).

V dvorazsežnem prikažemo lego točke s koordinatama ($x_{1},x_{2}$), vektor pa v obliki $\mathbf {x} =x_{1}~\mathbf {e} _{1}+x_{2}~\mathbf {e} _{2}$ kjer sta $\mathbf {e} _{1},\mathbf {e} _{2}$ bazna vektorja. Na podoben način lahko opišemo lego neke točke v krivočrtnem koordinatnem sistemu. Koordinate v tem sistemu pa označimo kot ($\xi ^{1},\xi ^{2}$). Vektor lege pa z $\mathbf {x} =\xi ^{1}~\mathbf {g} _{1}+\xi ^{2}~\mathbf {g} _{2}$. Količini $\xi ^{i}$ in $x_{i}$ sta povezani s preslikavo $\xi ^{i}=\varphi _{i}(x_{1},x_{2})$

Bazna vektorja $\mathbf {g} _{i}$ in $\mathbf {e} _{i}$ sta povezana z

$\mathbf {g} _{i}={\cfrac {\partial x_{1}}{\partial \xi ^{i}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial \xi ^{i}}}\mathbf {e} _{2}$.

Koordinatne črte so nivojske krivulje za $\xi ^{1}$ in $\xi ^{2}$ v dvorazsežni ravnini.

Zgled za krivočrtne koordinate je polarni koordinatni sistem. V tem primeru je preslikava enaka

$\xi ^{1}=r={\sqrt {x_{1}^{2}+x_{2}^{2}}}~;~~\xi ^{2}=\theta =\tan ^{-1}(x_{2}/x_{1})$

Splošna oblika krivočrtnih koordinat

Koordinatne ploskve, koordinatne smeri in koordinatne osi splošne oblike krivočrtnih koordinat.

V kartezičnem koordinatnem sistemu je lega točke P(x, y, z) določena s presekom treh med seboj pravokotnih ravnin x = konst., y = konst. z = konst. Koordinate x, y, in z so povezane s tremi novimi vrednostmi q₁, q₂ in q₃ z enačbami

x = x(q₁,q₂,q₃)     neposredna preslikava

y = y(q₁,q₂,q₃)     (krivočrtne v kartezične koordinate)

z = z(q₁,q₂,q₃).

Zgornje enačbe lahko zapišemo tudi kot

q₁ = q₁(x, y, z)     inverzna preslikava

q₂ = q₂(x, y, z)     (kartezične v krivočrtne koordinate)

q₃ = q₃(x, y, z).

Funkcija preslikav je bijektivna in zadovoljuje zahteve v domeni:

• funkcije so gladke
• determinanta obratne Jakobijeve matrike ni enaka nič.

To pa lahko zapišemo kot

$|J^{-1}|=\det {\partial (q_{1},q_{2},q_{3}) \over \partial (x,y,z)}={\begin{vmatrix}{\frac {\partial q_{1}}{\partial x}}&{\frac {\partial q_{1}}{\partial y}}&{\frac {\partial q_{1}}{\partial z}}\\{\frac {\partial q_{2}}{\partial x}}&{\frac {\partial q_{2}}{\partial y}}&{\frac {\partial q_{2}}{\partial z}}\\{\frac {\partial q_{3}}{\partial x}}&{\frac {\partial q_{3}}{\partial y}}&{\frac {\partial q_{3}}{\partial z}}\end{vmatrix}}\neq 0$.

Dano točko lahko opišemo tako, da podamo koordinate x, y in z ali pa koordinate q₁, q₂ in q₃. Inverzna enačba opisuje ploskev v novih koordinatah in presečišče treh ploskev določa lego točke v trirazsežnem prostoru. Ploskve q₁ = konstanta, q₂ = konstanta in q₃ = konstanta, se imenujejo koordinatne ploskve. Prostorske krivulje, ki jih dobimo na presečiščih dveh ploskev, pa so koordinatne črte. Koordinatne osi so določene kot tangente na koordinatne črte na preseku treh ploskev. To v splošnem stalne smeri v prostoru, kar velja za kartezične koordinate. Količina (q₁, q₂, q₃) so krivočrtne koordinate točke P(q₁, q₂, q₃).

V splošnem pa so (q₁, q₂,.... q_n) krivočrtne koordinate v n-razsežnem prostoru.

Zgled: Sferne koordinate

Koordinatne ploskve, koordinatne smeri in koordinatne osi sfernih koordinat. Ploskve: r - sfere, θ - stožci, φ - polravnine; smeri: r - straight beams, θ – vertikalni polkrogi, φ – horizontalne krožnice; osi: r – ravna smer, θ – tangente na vertikalne polkrožnice, φ – tangente na horizontalne krožnice.

Sferne koordinate so najpogosteje uporabljene krivočrtne koordinate. Krivočrtne koordinate (q₁, q₂, q₃).

V tem sistemu koordinate običajno označujemo z r (razdalja od pola, velja r ≥ 0), θ (zenitna razdalja ali širina 0 ≤ θ ≤ 180°) in φ (azimut ali dolžina 0 ≤ φ ≤ 360°).

Neposredna povezava med kartezičnimi in sfernimi koordinatami je

${\begin{aligned}x&=r\sin \theta \cos \phi \\y&=r\sin \theta \sin \phi \\z&=r\cos \theta \end{aligned}}$.

Z rešivijo za r, θ, in φ, dobimo obratne odnose med sfernimi in kartezičnimi koordinatami

${\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arccos \left({\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\right)\\\varphi &=\arctan \left({\frac {y}{x}}\right)\end{aligned}}$.

Krivočrtna lokalna baza

Pojem baze

Da bi definirali vektor s pomočjo koordinat potrebujemo še pojem baze. Baza je v trirazsežnem prostoru množica linearno neodvisnih vektorjev$\{\mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}\}$, ki jih imenujemo bazni vektorji. Vsak bazni vektor je povezan z eno koordinato pripadajoče razsežnosti. Vsak vektor $\mathbf {v}$ lahko prikažemo kot vsoto vektorjev $v_{i}~\mathbf {e} _{i}$, ki jih dobimo kot zmnožek baznega vektorja ($\mathbf {e} _{i}$) s skalarnim koeficientom ($v_{i}$), ki ga imenujemo komponenta. Vsak vektor ima natančno komponento v vsaki razsežnosti in ga lahko prikažemo kot

$\mathbf {v} =v_{1}~\mathbf {e} _{1}+v_{2}~\mathbf {e} _{2}+v_{3}~\mathbf {e} _{3}$.

Za takšen koordinatni sistem in njegovo bazo se zahteva, da je vsaj ena vrednost $v_{i}\neq 0$ velja

$v_{1}~\mathbf {e} _{1}+v_{2}~\mathbf {e} _{2}+v_{3}~\mathbf {e} _{3}\neq 0$. Ta pogoj se imenuje linearna neodvisnost.

Linearna neodvisnost pravi, da ne obstojajo bazni vektorji z velikostjo nič, ker bi v tem primeru dobili vektor z velikostjo nič, če bi ga množili s poljubno komponento. Nekoplanarni vektorji so linearno neodvisni. Katerikoli trije nekoplanarni vektorji lahko služijo kot baza v treh razsežnostih.

Bazni vektorji v krivočrtnih koordinatah

Za splošno obliko krivočrtnih koordinat se bazni vektorji in komponente spreminjajo od točke do točke. Poglejmo n-razsežni vektor $\mathbf {v}$, ki je izražen v kartezičnih koordinatah kot

$\mathbf {v} =v^{1}~\mathbf {e} _{1}+v^{2}~\mathbf {e} _{2}+v^{3}~\mathbf {e} _{3}+\dots +v^{n}~\mathbf {e} _{n}$.

Če spremenimo bazne vektorje v $\{\mathbf {g} _{1},\mathbf {g} _{2},\mathbf {g} _{3},\dots ,\mathbf {g} _{n}\}$ potem vektor $\mathbf {v}$ v novi bazi opisuje isti vektor

$\mathbf {v} ={\hat {v}}^{1}~\mathbf {g} _{1}+{\hat {v}}^{2}~\mathbf {g} _{2}+{\hat {v}}^{3}~\mathbf {g} _{3}+\dots +{\hat {v}}^{n}~\mathbf {g} _{n}$,

kjer so

• ${\hat {v}}^{i}$ komponente vektorja v novi bazi.

Torej je vsota, ki opisuje vektor $\mathbf {v}$ v novi bazi je sestavljena iz drugih vektorjev, vsota pa ostane enaka.

Kovariantna in kontravariantna baza

Bazne vektorje lahko povežemo s koordinatnim sistemom na dva načina

• lahko jih postavimo tako, da so kolinearni z osmi
• lahko jih postavimo tako, da so pravokotni (normalni) na koordinatne ploskve.

V prvem primeru se vektorji transformirajo kot kovariantni vektorji. V drugem primeru se bazni vektorji transformirajo kot kontravariantni vektorji. Pri označevanju teh dveh vrst baznih vektorjev uporabljamo dva načina. Kovariantne vektorje označujemo s spodnjimi oznakami, kontravariantne vektorje pa označujemo z zgornjimi oznakami. To pomeni, da v odvisnosti od tega kako jih zgradimo, imamo za splošne krivočrtne koordinate dve skupini baznih vektorjev v vsaki točki: $\{\mathbf {g} _{1},\mathbf {g} _{2},\mathbf {g} _{3}\}$ za kovariantno bazo in $\{\mathbf {g} ^{1},\mathbf {g} ^{2},\mathbf {g} ^{3}\}$ za kontravariantno bazo.

Vektor $\mathbf {v}$ lahko izrazimo v katerikoli bazi

$\mathbf {v} =v^{1}\mathbf {g} _{1}+v^{2}\mathbf {g} _{2}+v^{3}\mathbf {g} _{3}=v_{1}\mathbf {g} ^{1}+v_{2}\mathbf {g} ^{2}+v_{3}\mathbf {g} ^{3}$.

Pri tem je lahko vektor $\mathbf {v}$ kovarianten ali kontravarianten v odvisnosti od vrste njegovih komponent.

Zunanje povezave

• Krivočrtne koordinate na MathWorld (angleško)
• Prof. R. Brannon - e-knjiga o krivočrtnih koordinatah (angleško)