Zeemanov pojav

Zeemanov pojav je fizikalni pojav, ki se kaže v razcepitvi spektralnih črt ob prisotnosti statičnega zunanjega magnetnega polja. Podoben je Starkov pojav, ki pa se pojavlja ob prisotnosti zunanjega električnega polja.

Kadar pojav opazujemo na absorbcijskih spektralnih črtah, se pojav imenuje obratni Zeemenov pojav.

Pojav se imenuje po nizozemskem fiziku Pieteru Zeemanu (1865 – 1943), ki ga je prvi opazil.

Razcepitev spektralnih črt

Razcepitev v magnetnem polju. Levi del slike prikazuje energijske nivoje brez zunanjega magnetnega polja, desni del pa energijske nivoje ob prisotnosti zunanjega magnetnega polja.

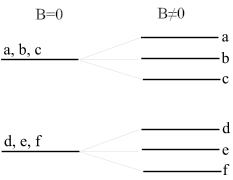
Šibko magnetno polje (običajni ali normalni Zeemanov pojav)

Elektron lahko obravnavamo kot električni tok ($I = \frac{\mathrm{d}Q}{\mathrm{d}t}$ kar lahko zapišemo $I = \frac{Q}{t}$ z $Q = - e \,$ in $v = \frac{2\pi r}{t}$)

dobimo

$I = - e \cdot \frac{v}{2\pi r}$.

Ta tok povzroča magnetni moment

$\vec{\mu_l} = I \cdot \vec{S} = -e v \frac{r}{2} \cdot \hat{n}$.

kjer je

• $\vec{S} \,$ vektor površine
• $\hat{n} \,$ na površino pravokoten enotski vektor

Za magnetni moment elektrona dobimo

$\vec{\mu_\mathrm{l}} = -\frac{e}{2 m_\mathrm{e}} \, \vec{l}$

Kar dobimo iz izraza za vrtilno količino

$\vec{\mu_\mathrm{l}} = -\frac{e}{2 m_\mathrm{e}} \, \vec{l}$.

Potencialna energija elektrona v magnetnem polju je $E_\mathrm{pot} = - \vec{\mu_\mathrm{l}} \cdot \vec{B}$ oziroma

$E_\mathrm{pot} = \frac{e}{2 m_\mathrm{e}} \vec{l} \cdot \vec{B}$

kjer je

• $\vec B \,$ vektor gostote magnetnega polja
• $m_{e} \,$ masa elektrona

Ta vrednost predstavlja energijski razcep zaradi zunanjega magnetnega polja.

Če predpostavimo, da ima magnetno polje smer osi-z in vzamemo za vrtilno količino vrednost, ki je kvantizirana (magnetno kvantno število) $l_z = m \hbar$, kjer je $m \,$ celo število), potem dobimo

$E_\mathrm{pot} = \frac{e \hbar}{2 m_\mathrm{e}}m \, B = m \,\mu_\mathrm{B} B$

kjer je

• $m \,$ magnetno kvantno število
• $\mu_B \,$ Bohrov magneton
• $B \,$ gostota magnetnega polja
• $\hbar \,$ reducirana Planckova konstanta
• $m_{e} \,$ masa elektrona

Energijski nivoji se razcepijo na $2l+1 \,$ vrednosti, ki odgovarjajo magnetnim kvantnim številom $m = -l, \ldots , 0, \ldots , l \,$.

Pri normalnem Zeemanovem pojavu ne upoštevamo spina elektrona. Polarizacija posameznih črt je različna za opazovanje vzdolž magnetnega polja in za opazovanje pravokotno na magnetno polje .

Anormalni Zeemanov pojav

Običajni Zeemenov pojav kaže razcep na tri enako oddaljene spektralne črte (tripleti). Pri neobičajnem (nenormalnem) Zeemanovem pojavu pa opažamo cepitev na štiri, šest ali celo več črt. Ta pojav imenujemo anormalni Zeemanov pojav.

Izraz anormalni ima zgodovinski izvor. V času, ko so ga odkrili, še niso poznali spina, in so ga zaradi tega imenovali anormalni.

Anormalni Zeemanov pojav nastane takrat, ko je skupni spin vseh elektronov različen od 0. Pri anormalnem Zeemanovem pojavu je torej potrebno upoštevati tudi spin oziroma spinsko tirno sklopitev. Magnetna momenta sta v tem primeru: Magnetni moment zaradi tirne vrtilne količine je enak:

$\vec{\mu}_\mathrm{L} = -\frac{\mu_\mathrm{B}}{\hbar}\, \vec{L}$

Magnetni moment zaradi spinske vrtilne količine pa je:

$\vec{\mu}_\mathrm{S} = -g_\mathrm{s}\frac{\mu_\mathrm{B}}{\hbar}\, \vec{S}.$

$\vec{\mu}_\mathrm{J} = \vec{\mu}_\mathrm{S} + \vec{\mu}_\mathrm{L} = -\frac{\mu_\mathrm{B}}{\hbar} \left( g_\mathrm{s}\vec{S} + \vec{L}\right),$

kjer je

• $g_\mathrm{s} \approx 2$

Magnetni moment $\vec \mu_J \,$ in vrtilna količina $\vec J = \vec L + \vec S \,$ nista več vzporedna. Vrtilna količina in magnetni moment precesirata okoli osi z.

Iz kvantnomehanske teorije motenj sledi, da je energijska razlika dveh sososednjih energijskih novojev enaka

$\Delta E_\mathrm{B} = m_J \mu_\mathrm{B} g_\mathrm{J} B\!\,,$

kjer je

• $g_J = 1 + \frac{J(J+1) + S(S+1) - L(L+1)}{2J(J+1)}.$
• $m_j \,$ magnetno kvantno število
• $J \,$ skupna vrtilna količina
• $g_j \,$ Landéjev množitelj g za skupno vrtilno količino

Razcepitev vodikovih črt v magnetnem polju

Razcep energijskih nivojev v zunanjem magnetnem polju in prehodi med njimi (desni del slike). Na levi strani so prikazani energijski nivoji brez prisotnosti zunanjega magnetnega polja.

Cepitev spektralnih črt vodikovega atoma zaradi zunanjega magnetnega polja.

Lymanov alfa prehod brez magnetnega polja omogoča dva prehoda

$2P_{1/2} \to 1S_{1/2}\,$

$2P_{3/2} \to 1S_{1/2}\,$

Če se snov nahaja v zunanjem magnetnem polju je teh prehodov veliko več, ker se energijska stanja razcepijo. Stanje $1P_{1/2}\,$ se razcepi na 2 nivoja in stanje $2P_{1/2}\,$ na 4 nivoje z $m_j = 3/2, 1/2, -1/2, -3/2 \,$.
Landéjev množitelj g je enak

$g_J = 2 \,$ za stanje $1S_{1/2}\,$ ( za $j=1/2, l=0 \,$)

$g_J = 2/3 \,$ za stanje $2P_{1/2} \,$ ( za $j=1/2, l=1 \,$)

$g_J = 4/3 \,$ za stanje $2P_{3/2} \,$ ( za $j=3/2, l=1 \,$).

Močno magnetno polje

V izredno močnem magnetnem polju se pojavi dodatna cepitev spektralnih črt. Dodatna cepitev je posledica porušitve sklopljenosti spinske in tirne vrtilne količine. Vpliv spinske vrtilne količine postane zanemarljiv. Obe vrtilni količini postaneta močneje povezani s smerjo zunanjega magnetnega polja. V šibkem magnetnem polju vektorja spinske in tirne vrtilne količine kažeta precesijo, ki ni povezana z zunanjim magnetnim poljem.

Kvadratni Zeemanov pojav

V izredno močnih zunanjih magnetnih poljih se pojavi vpliv druge potence na razcepitev energijskih nivojev. Magnetni moment postane odvisen od kvadrata magnetnega polja.

$\Delta E \propto B^2 \,$

Uporaba

V astrofiziki je prvi opazil Zeemanov pojav ameriški astronom in strokovnjak za astronomijo Sonca George Ellery Hale (1868 – 1938) v področjih Sončevih peg. Prvi je opravil meritve Zeemanovega pojava na zvezdi ameriški astronom Horace Welcome Babcock (1912 – 2003) v letu 1947. Sedaj se s pomočjo Zeemenovega pojava spremljajo magnetna polja na Soncu s pomočjo satelita SOHO (Solar and Heliospheric Observatory). Za opazovanja magnetnih polja na zvezdah se uporablja zvezdni spektropolarimeter ESPaDOns , ki se nahaja v Franciji, ter Kanadsko francosko havajski teleskop in NARVAL . Zeemanov pojav se uporablja tudi v elektronski spinski resonanci, jedrski spinski resonanci, Mössbauerjavi spektroskopiji ter na mnogih drugih področjih.

Zunanje povezave

• Zeemanov pojav (v angleščini)
• Opis Zeemanovega pojava (v angleščini)