Načelo vključitev in izključitev

Načelo vključitev in izključitev je v kombinatoriki, veji matematike, preštevalna tehnika, ki posploši pogosto metodo pridobivanja števila elementov unije dveh končnih množic. S simboli se to zapiše:

|A\cup B|=|A|+|B|-|A\cap B|\!\,,

kjer sta A in B dve končni množici, |S| pa označuje kardinalnost množice S (ki se lahko pri končni množici obravnava kot število elementov). Formula izraža dejstvo, da je včasih vsota elementov dveh množic prevelika, saj se je lahko nekaj elementov štelo dvakrat. Ti elementi se nahajajo v preseku dveh množic. Izračun se popravi z odštevanjem velikosti preseka.

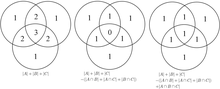
Načelo se veliko bolje vidi na primeru treh množic, ki je za tri množice A, B in C podano s:

|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|\!\,.

Ta formula se lahko potrdi s tem, da se prešteje kolikokrat se je preštelo vsako območje Vennovega diagrama na desni strani formule. V tem primeru, ko se odstrani prevečkrat štete elemente, je treba nazaj prišteti, saj sse je odštelo prevečkrat.

Načelo vključitev in izključitev na Vennovem diagramu za tri množice

Rezultate zgornjih primerov, ki so se podali za razlago načela vključitev in izključitev, se sedaj posploši. Da se najde kardinalnost unije $n$ množic:

se vključi kardinalnost vseh množic.
izključi se kardinalnosti presekov med pari.
vključi se kardinalnosti presekov med trojicami.
izključi se kardinalnosti presekov med četvericami.
vključimo se kardinalnosti presekov med petimi množicami.
se nadaljuje, dokler se ne vključi (če je $n$ lih) ali izključi (če je $n$ sod) kardinalnosti presekov med $n$ množicami.

Ime prihaja iz zamisli, da načelo temelji na pretiranem vključevanju, ki mu sledi pretirano izključevanje. Koncept je zasnoval Abraham de Moivre leta 1718,^[1] toda v delu se je prvič pojavilo pri matematiku Danielu da Silvi leta 1854,^[2] kasneje pa v delu Jamesa Josepha Sylvestra leta 1883.^[3] Zaradi te uporabe se včasih formulo pripisuje Da Silvi ali Sylvestru. Načelo je primer metode sita, ki se zelo uporablja v teoriji števil in se včasih navede kot formula sita,^[3] toda Legendre je že uporabil podobno napravo v kontekstu sita leta 1808.

Izrek

V svoji splošni obliki, načelo vključitev in izključitev za končne množice $A 1, ..., A n$ pravi:

\left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{i=1}^{n}|A_{i}|-\sum _{1\leqslant i<j\leqslant n}|A_{i}\cap A_{j}|+\sum _{1\leqslant i<j<k\leqslant n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.

(1)

Vsak člen v formuli načelu vključitev in izključitev se postopoma popravi, dokler niso vsa območja Vennovega diagrama prešteta točno enkrat.

To se lahko zapiše kot:

\left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leqslant i_{1}<\cdots <i_{k}\leqslant n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)\!\,,

ali:

\left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{\emptyset \neq J\subseteq \{1,\ldots ,n\}}(-1)^{|J|+1}\left|\bigcap _{j\in J}A_{j}\right|\!\,.

Drugače rečeno z besedami: če se želi prešteti število elementov v končni uniji končnih množic, je treba najprej sešteti vse kardinalnosti posameznih množic, potem odšteti število elementov, ki se pojavijo v najmanj dveh množicah, nato je treba prišteti število elementov, ki se pojavijo v najmanj treh množicah in odšteti število elementov, ki se pojavijo v najmanj štirih množicah ter tako naprej. Ta proces se vedno konča, saj na koncu ni več elementov, ki bi se pojavili v več množicah, kot jih je v uniji množic. (Na primer za $n=4\!\,$ ne more biti nobenih elementov več, ki bi se pojavili v več kot $4\!\,$ množicah; enako ne more biti več elementov, ki bi se pojavili v najmanj $5\!\,$ množicah.)

V uporabi je pogosto, da je načelo izraženo v komplementarni obliki. Naj bo $S$ končna univerzalna množica, ki vsebuje vse $A i$ in naj bo ${\bar {A_{i}}}$ komplement od $A i$ v $S$ . Po De Morganovih zakonih se dobi:

\left|\bigcap _{i=1}^{n}{\bar {A_{i}}}\right|=\left|S-\bigcup _{i=1}^{n}A_{i}\right|=|S|-\sum _{i=1}^{n}|A_{i}|+\sum _{1\leqslant i<j\leqslant n}|A_{i}\cap A_{j}|-\cdots +(-1)^{n}|A_{1}\cap \cdots \cap A_{n}|\!\,.

Naslednja različica izreka je taka: naj bodo $P 1, ..., P n$ značilnosti, ki jih elementi iz $S$ lahko imajo ali pa ne. Po tem načelo vključitev in izključitev poda način izračuna števila elementov iz $S$ , ki nimajo nobene izmed teh značilnosti. Naj bo $A i$ podmnožica elementov iz $S$ , ki imajo značilnost $P i$ , uporabi pa se načelo v svoji komplementarni obliki. To različico odkril Sylvester.^[1]

Če se vzame le prvih $m<n$ vsot na desni (v splošni obliki načela), potem bo rešitev prevelika, če je $m$ lih in premajhen, če je $m$ sod.

Zgledi

Štetje celih števil

Kot preprost primer načela vključitve in izključitve, sledi naslednje vprašanje:^[2]

Koliko naravnih števil iz {1,...,100} ni deljivih z 2, 3 ali 5?

Naj bo S = {1,...,100} in P₁ značilnost, da je naravno število deljivo z 2, P₂ značilnost za deljivost s 3 in P₃ značilnost za deljivost s 5. Če je A_i podmnožica od S, katerih elementi imajo značilnost P_i, se dobi elementarno štetje: |A₁| = 50, |A₂| = 33 in |A₃| = 20. Obstaja 16 izmed teh naravnih števil, ki so deljiva s 6 in 10, ki so deljiva z 10 ter 5, ki so deljiva s 15. Na koncu so le 3 naravna števila, ki so deljiva s 30, torej je število vse naravnih števil, ki niso deljiva z 2, 3, ali 5 podano z:

100 − (50 + 33 + 20) + (16 + 10 + 6) - 3 = 26.

Glej tudi

Viri

Adams, Henry; Emmrich, Kelly; Gillespie, Maria; Golden, Shannon; Pries, Rachel (2021), »Counting Rocks! An Introduction to Combinatorics«, Državna univerza Kolorada, arXiv:2108.04902
Allenby, R. B. J. T.; Slomson, Alan (2010), How to Count: An Introduction to Combinatorics, Discrete Mathematics and Its Applications (2 izd.), CRC Press, str. 51–60, ISBN 9781420082609
Björklund, A.; Husfeldt, T.; Koivisto, M. (2009), »Set partitioning via inclusion–exclusion«, SIAM Journal on Computing, 39 (2): 546–563, doi:10.1137/070683933
Brualdi, Richard A. (2010), Introductory Combinatorics (5. izd.), Prentice–Hall, ISBN 9780136020400
Cameron, Peter J. (1994), Combinatorics: Topics, Techniques, Algorithms, Cambridge University Press, ISBN 0-521-45761-0
Fernández, Roberto; Alan D., Sokal; Fröhlich, Jürg (1992), Random Walks, Critical Phenomena, and Triviality in Quantum Field Theory, Texts an Monographs in Physics, Berlin: Springer-Verlag, str. xviii+444, ISBN 3-540-54358-9, MR 1219313, Zbl 0761.60061
Graham, R. L.; Grötschel, M.; Lovász, L. (1995), Hand Book of Combinatorics (volume-2), MIT Press – North Holland, ISBN 9780262071710
Gross, Jonathan L. (2008), Combinatorial Methods with Computer Applications, Chapman&Hall/CRC, ISBN 9781584887430
»Inclusion-and-exclusion principle«. Encyclopedia of Mathematics. EMS Press. 2001 [1994].
Mazur, David R. (2010), Combinatorics A Guided Tour, The Mathematical Association of America, ISBN 9780883857625
Roberts, Fred S.; Tesman, Barry (2009), Applied Combinatorics (2. izd.), CRC Press, ISBN 9781420099829
Stanley, Richard P. (1986), Enumerative Combinatorics Volume I, Wadsworth & Brooks/Cole, ISBN 0534065465
van Lint, J. H.; Wilson, R. M. (1992), A Course in Combinatorics, Cambridge University Press, ISBN 0521422604

Ta članek vsebuje material iz principle of inclusion–exclusion na PlanetMath, ki ima licenco Creative Commons Attribution/Share-Alike License.

[robe_2009-1] 1,0 ^1,1 Roberts; Tesman (2009).

[mazu_2010-2] 2,0 ^2,1 Mazur (2010).

[vanl_1992-3] 3,0 ^3,1 van Lint; Wilson (1992).

[1]

[2]

[3]