Hessov zakon

Hessov zákon [hésov ~] je eden od osnovnih zakonov termodinamike. Ime je dobil po svojem utemeljitelju, v Švici rojenemu ruskemu kemiku in zdravniku Germainu Henriju Hessu. Zakon obravnava spremembo energije in pravi, da je
- sprememba energije odvisna samo od začetnega in končnega stanja sistema in je neodvisna od poti, po kateri je do spremembe prišlo.
Hessov zakon omogoča izračun energetskih sprememb, ki se jih sicer ne da enostavno izmeriti.
Razlaga[uredi | uredi kodo]
Hessov zakon trdi, da je sprememba energije v vsakem kemičnem ali fizikalnem procesu neodvisna od poti in števila vmesnih korakov, ki so potrebni, da se proces zaključi. Z drugimi besedami to pomeni, da sta za spremembo energije pomembni samo začetno in končno stanje sistema.
Neodvisnost od poti velja tudi za vse druge funkcije, ki so povezane s stanjem sistema, na primer za entropijo in prosto energijo.
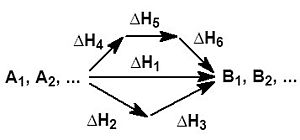
Na zgornji sliki je shematski prikaz kemijske reakcije, v kateri iz reaktantov A1, A2... nastanejo produkti B1, B2... Reakcija lahko poteka po treh različnih poteh, ki imajo različno število korakov. Spremembo energije, bolj pravilno entalpije (ΔH), zapišemo z enačbo:
Hessov zakon omogoča izračunavanje spremembe entalpije tudi takšnih reakcijah, katerih spremembe entalpije se ne da izmeriti neposredno. Za takšen izračun je potrebna urejena kemijska enačba ali sistem enačb in poznavanje tvorbenih entalpij (ΔHt) reagentov in reaktantov.
Kemijske enačbe se obnašajo zelo podobno kot matematični sistem linearnih enačb: lahko se delijo ali množijo s celimi števili, seveda pa je treba istočasno deliti ali množiti tudi vrednosti entalpij. Če se smer reakcije obrne, se predznak entalpije spremeni, na primer iz ΔH v –ΔH in obratno.
Če je celotna sprememba entalpije negativna (ΔHr<0), je reakcija eksotermna in obratno: če je sprememba entalpije pozitivna (ΔHr>0), je reakcija endotermna. Za ugotavljanje spontanosti reakcij igra pomembno vlogo entropija, to pa pomeni, da so reakcije lahko spontane, četudi je sprememba entalpije pozitivna!
Hessov zakon pravi, da so spremembe entalpije aditivne. Iz tega sledi, da se lahko ΔH posamezne reakcije izračuna iz razlike med tvorbenimi entalpijami produktov in reaktantov. Razliko zapišemo z enačbo:
Za sestavljene ali stopenjske reakcije se malo spremeni oblika zapisa, koncept pa ostane isti:
Uporaba[uredi | uredi kodo]
Če poznamo tvorbene entalpije (ΔHt) vseh reaktantov in produktov, ki sodelujejo v kemijski reakciji, lahko spremembo entalpije reakcije izračunamo z enačbo:
Če je reakcija na primer gorenje (sežig), lahko enačbo priredimo in jo zapišemo kot:
Zgled enostavnega izračuna[uredi | uredi kodo]
Kakšna je standardna reakcijska entalpija reakcije
- CH4(g) + 2O2(g) → CO2(g) + 2H2O(l)?
Za izračun potrebujemo standardne tvorbene entalpije vseh reaktantov in produktov:
| Spojina | ΔHt0 [kJ mol-1] |
|---|---|
| CH4(g) | -75 |
| O2(g) | 0 |
| CO2(g) | -394 |
| H2O(l) | -286 |
Izračun:
- ΔH0r = ΔH0sež = [-394 + 2(-286)] - [-75 + 2(0)] = -891 kJ mol-1
Zgled bolj zapletenega izračuna[uredi | uredi kodo]
Kakšna je ΔHr reakcije:
- 2B(s) + (3/2)O2(g) → B2O3(s)
Podatki:
- B2O3(s) + 3H2O(g) → 3O2(g) + B2H6(g) ΔH = +2035 kJ
- H2O(l) → H2O(g) ΔH = +44 kJ
- H2(g) + (1/2)O2(g) → H2O(l) ΔH = -286 kJ
- 2B(s) + 3H2(g) → B2H6(g) ΔH = +36 kJ
Izračun:
Prvo enačbo obrnemo, drugo in tretjo enačbo pa pomnožimo s 3. Zapis bo zdaj izgledal takole:
- B2H6(g) + 3O2(g) → B2O3(s) + 3H2O(g) ΔH = -2035 kJ
- 3H2O(g) → 3H2O(l) ΔH = -132 kJ
- 3H2O(l) → 3H2(g) + (3/2)O2(g) ΔH = +858 kJ
- 2 B(s) + 3H2(g) → B2H6(g) ΔH = +36 kJ
Enačbe seštejemo in črtamo izraze, ki so na obeh straneh enačbe enaki. Rezultat je naslednja enačba:
- 2B(s) + (3/2)O2(g) → B2O3(s) ΔH = -1273 kJ
Odgovor:
Reakcijska entalpija ΔHr je -1273 kJ. ΔHr je istočasno enaka tvorbeni entalpiji ΔHt B2O3(s).
Razširitev na entropijo in prosto energijo[uredi | uredi kodo]
Koncepti Hessovega zakona se lahko razširijo na spremembe entropije in proste energije, ki sta tudi funkciji stanja. Primer take razširitve je Bordwellov termodinamski ciklus, ki izkorišča enostavno izmerjena ravnotežja in redoks potenciale za določanje eksperimentalno nedostopnih vrednosti Gibbsove proste energije. S kombiniranjem vrednosti ΔG0 iz Bordwellovih termodinamskih ciklusov in vrednosti ΔH0, dobljenih s Hessovim zakonom, se lahko določijo vrednosti entropij, ki se ne dajo izmeriti neposredno in se morajo zato izračunati po drugih poteh.
Za entropijo velja, da je:
Za prosto energij velja, da je:
Viri[uredi | uredi kodo]
- Leicester, Henry M. (1951). "Germain Henri Hess and the Foundations of Thermochemistry". The Journal of Chemical Education 28: 581 – 583.
- Glasstone, Samuel. Textbook of Physical Chemistry, 2. izdaja, Naučna knjiga, Beograd (1967), str. 153-159









