Skakačev obhod
Videz
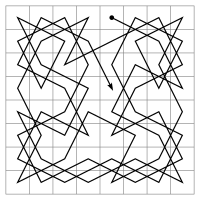



Skakačev obhod je matematični problem s skakačem na standardni šahovnici (8×8). Skakača postavimo na poljubno začetno polje in z njim obiščemo vsa ostala polja na deski.
Obstaja več milijard rešitev. V okoli 122.000.000 rešitvah se skakač vrne na isto polje, od koder je začel.
Problem, ki so ga proučevali mnogi matematiki, tudi Euler, lahko posplošimo v več smeri:
- iščemo zaključene obhode (po zadnji potezi skakač skoči na začetno polje),
- uporabimo različne velikosti (in oblike) šahovnice,
- uporabimo drugačne šahovske figure,
- uporabimo drugačno topologijo šahovnice.
Obstajajo tudi igre za enega ali več igralcev na to temo.
Skakačev obhod je primer bolj splošnega iskanja Hamiltonove poti v teoriji grafov, ki je NP-poln. Zaključen skakačev obhod pa je primer Hamiltonovega cikla.
Program v paskalu
[uredi | uredi kodo] program lipicanec(output);
[[Niklaus Wirth|Wirth N.]], Računalniško programiranje I}
const n=8;
nsq=n*n; {deska 8x8}
xz=1; yz=1; {zacetni koordinati}
type index=1...n;
var i,j : integer;
q : boolean;
s : set of index;
a,b : array[1...8] of integer; {osem moznih skokov}
h : array[index,index] of integer;
m : integer;
procedure izpis; {resitve}
var i,j:integer;
begin
for i:=1 to n do begin
for j:=1 to n do write(h[i,j]:4);
writeln;
end;
end; {izpis}
procedure try(i:integer; x,y:index; var q:boolean);
var k,u,v : integer; q1:boolean;
begin
k:=0;
repeat
k:=k+1; q1:=false;
u:=x+a[k]; v:=y+b[k];
if (u>=1) and (u<=n) and (v>=1) and (v<=n) then
if h[u,v]=0 then begin
h[u,v]:=i;
if i<nsq then begin
try(i+1,u,v,q1); {rekurzivni klic}
if not q1 then h[u,v]:=0;
end else
q1:=true;
end;
until (q1 or (k=8));
q:=q1;
end;{try}
begin
s:=[1...n];
begin
a[1]:= 2; b[1]:= 1;
a[2]:= 1; b[2]:= 2;
a[3]:=-1; b[3]:= 2;
a[4]:=-2; b[4]:= 1;
a[5]:=-2; b[5]:=-1;
a[6]:=-1; b[6]:=-2;
a[7]:= 1; b[7]:=-2;
a[8]:= 2; b[8]:=-1;
for i:=1 to n do
for j:=1 to n do begin h[i,j]:=0; end;
h[xz,yz]:=1;
try(2,xz,yz,q);
if q then izpis else writeln('Ni rešitve!');
end;
end.
