Magična konstanta
Mágična konstánta ali tudi mágična vsôta magičnega kvadrata je vsota števil v vsaki vrstici, stolpcu in (glavni) diagonali magičnega kvadrata. Magična konstanta spodaj prikazanega magičnega kvadrata je 15.
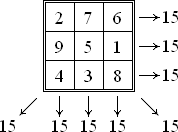
Izraz magična konstanta ali magična vsota je podobno povezan tudi z drugimi »magičnimi« figurami, kot so npr. magične zvezde, magične kocke ali magični teserakti, oziroma hiperkocke.
Normalni magični kvadrati[uredi | uredi kodo]
Če je magični kvadrat reda n normalen (vsebuje števila od 1 do n²), potem je magična konstanta odvisna le od vrednosti n. Njena vrednost je:
Ta obrazec je posledica obrazca za vsoto prvih n celih števil:
ki da za primer k = n² vrednost n²(n²+1)/2, kar je potem deljeno z n, ker obstaja n vrstic, katerih vsota je enaka.
Magične konstante normalnih magičnih kvadratov reda n = 3, 4, 5, … so (OEIS A006003):
Števila v vsaki vrstici, stolpcu ali diagonali normalnega magičnega kvadrata tvorijo magično vrsto.
Magične kocke[uredi | uredi kodo]
Podobno, če magična kocka vsebuje števila 1, 2, ..., n³, je njena magična konstanta (A027441):
Magični teserakti[uredi | uredi kodo]
V štirih razsežnostih magični teserakt vsebuje števila 1, 2, ..., n4, njegova magična konstanta je:
Magične hiperkocke[uredi | uredi kodo]
V splošnem vsebujejo magične hiperkocke razsežnosti k in reda n števila 1, 2, ..., nk, njihova magična konstanta pa je:
Magične zvezde[uredi | uredi kodo]
Magična konstanta normalne magične zvezde, ki vsebuje cela števila od 1 do 2n, na n točkah je:
Glej tudi[uredi | uredi kodo]
Zunanje povezave[uredi | uredi kodo]
- 260 kot magična konstanta problema osmih dam in magičnih kvadrataov 8 × 8 Arhivirano 2005-03-19 na Wayback Machine. (angleško)
- Matematični obrazci za hiperkocko (angleško)






