Darcy-Weisbachova enačba
Darcy-Weisbachova enačba je v hidravliki namenjena za računanje tlačnih izgub v ravnih ceveh krožnega preseka zaradi upora pri toku tekočine:
oziroma izgube tlačne višine:
kjer so:
- λ ... koeficient trenja,
- l ... dolžina cevi [m],
- d ... premer cevi [m],
- v ... pretočna hitrost [m/s],
- ρ ... gostota tekočine [kg/m³],
- g ... težni pospešek [m/s²].
Koeficientu:
rečejo koeficient krajevnih izgub. Darcy-Weisbachova enačba velja za vse vrste tokov. S koeficientom ζ lahko Darcy-Weisbachovo enačbo zapišemo kot
oziroma
Pri znanem pretoku Q [m³/s] skozi ravno cev krožnega preseka lahko določimo tlačne izgube po enačbi
oziroma
Koeficient trenja je odvisen od brezrazsežnega Reynoldsovega števila Re in od relativne hrapavosti cevi k/d, kjer je k absolutna hrapavost stene cevi in je odvisna od materiala in kakovosti cevi:
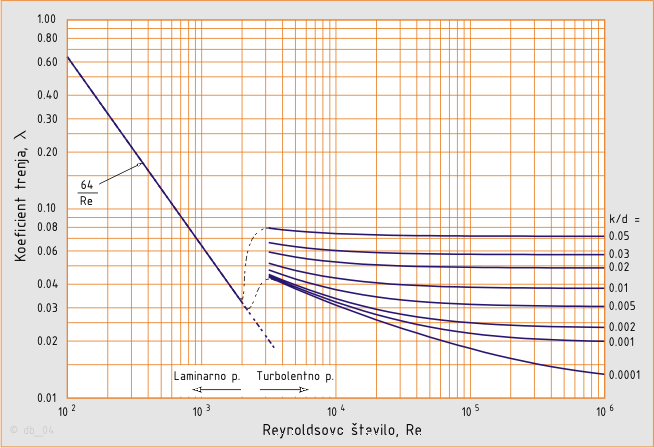
V laminarnem področju (Re < 2320) je koeficient trenja odvisen od Reynoldsovega števila Re in faktorja oblike cevi φ (za krožne cevi znaša 1):
V turbolentnem področju (Re > 2320) pa je koeficient trenja odvisen od Reynoldsovega števila in od relativne hrapavosti cevi k/d. Tukaj ga določamo analitično po znanih enačbah (Prandtl-Kármánova, Colebrook-Whiteova, Nikuradsejeva) ali pa grafično s pomočjo Moodyjevega diagrama.
Enačba se imenuje po Henryju Philibertu Gaspardu Darcyju, ki je enačbo najprej razvil iz Pronyjeve enačbe, leta 1845 pa jo je v današnji obliki zapisal Julius Weisbach. Z enačbo se je ukvarjalo veliko avtorjev in bi se praviloma morala imenovati s kar dolgim imenom.

![{\displaystyle \Delta p_{i}=\lambda \rho {l \over d}{{v^{2}} \over 2}\quad \left[\mathrm {Pa} \right]\qquad (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4f8360868cb70845da04556af8016c33eb0374d)
![{\displaystyle h_{i}=\lambda {l \over d}{{v^{2}} \over {2g}}\quad \left[\mathrm {m} \right]\qquad (2),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c06cf36478274c54728999f9721e7c47b5017273)

![{\displaystyle \Delta p_{i}=\zeta \rho {{v^{2}} \over 2}\quad \left[\mathrm {Pa} \right]\qquad (4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e95d4a925eebf3c2d9159e6b9ae561838c8d45a0)
![{\displaystyle h_{i}=\zeta {{v^{2}} \over {2g}}\quad \left[\mathrm {m} \right]\qquad (5).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c138d01d9c6e38de8afb5a98d45c1bec69365510)
![{\displaystyle \Delta p_{i}={{8\lambda \rho lQ^{2}} \over {\pi ^{2}d^{5}}}\quad \left[\mathrm {Pa} \right]\qquad (6)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eef53ad44adb2fda75577e37f8a00af83634e368)
![{\displaystyle h_{i}={{8\lambda lQ^{2}} \over {\pi ^{2}gd^{5}}}\quad \left[\mathrm {m} \right]\qquad (7).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a567f9c723e31cb0a4186a004217d62224114e10)