Meja proizvodnih možnosti
Meja proizvodnih možnosti (MPM), krivulja proizvodnih možnosti (KPM) ali transformacijska krivulja/meja je krivulja, ki prikazuje različne kombinacije količin dveh dobrin, ki ju je mogoče proizvajati v okviru danih virov in tehnologije. Gre za grafični prikaz, ki prikazuje vse možnosti proizvodnje dveh izdelkov, ki ju je mogoče proizvajati z uporabo vseh proizvodnih dejavnikov, pri čemer so dani viri na enoto časa v celoti in učinkovito izkoriščeni. MPM ponazarja več ekonomskih pojmov, kot so alokacijska učinkovitost, ekonomija obsega, oportunitetni stroški (ali mejna stopnja transformacije), proizvodna učinkovitost in pomanjkanje virov (osnovni ekonomski problem, s katerim se soočajo vse družbe).[1]
Ta kompromis se običajno obravnava za gospodarstvo, vendar velja tudi za vsakega posameznika, gospodinjstvo in gospodarsko organizacijo. Eno dobrino je mogoče proizvajati le tako, da se viri preusmerijo z drugih dobrin, torej tako, da se jih proizvaja manj.
Krivulja MPM, ki grafično omejuje proizvodni nabor za fiksne vhodne količine, prikazuje največjo možno raven proizvodnje ene dobrine za vsako določeno raven proizvodnje druge dobrine ob upoštevanju obstoječega stanja tehnologije. S tem opredeljuje proizvodno učinkovitost v okviru tega proizvodnega nabora: točka na meji pomeni učinkovito uporabo razpoložljivih vložkov (npr. točke B, D in C na grafu), točka pod krivuljo (npr. A) pomeni neučinkovitost, točka zunaj krivulje (npr. X) pa pomeni nezmožnost.
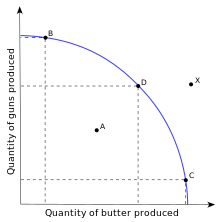
Krivulje MPM se običajno rišejo kot izbočene navzgor ali navzven od izvora (»konkavne«, če jih gledamo od izvora), lahko pa so prikazane kot izbočene navzdol (navznoter) ali linearne (ravne), kar je odvisno od številnih predpostavk.
Premik MPM navzven je posledica rasti razpoložljivosti vložkov, kot sta fizični kapital ali delo, ali tehnološkega napredka v znanju o tem, kako vložke pretvoriti v rezultate. Takšen premik na primer odraža gospodarsko rast, ki že deluje s polno produktivnostjo (na MPM), kar pomeni, da se lahko v določenem časovnem obdobju proizvede več obeh proizvodov, ne da bi pri tem trpela proizvodnja katere koli dobrine. Nasprotno pa se bo MPM premaknila navznoter, če se zmanjša delovna sila, če se izčrpa zaloga surovin ali če se zaradi naravne nesreče zmanjša zaloga fizičnega kapitala. Večina gospodarskih krčenj pa ne izraža tega, da je mogoče proizvesti manj, ampak da je gospodarstvo začelo delovati pod mejo, saj sta običajno tako delovna sila kot fizični kapital nezadostno zaposlena in zato ostajata neizkoriščena.
V mikroekonomiji MPM prikazuje možnosti, ki jih ima posameznik, gospodinjstvo ali podjetje v svetu dveh dobrin. Po definiciji je vsaka točka na krivulji proizvodno učinkovita, vendar bodo zaradi narave tržnega povpraševanja nekatere točke bolj dobičkonosne kot druge. Ravnovesje za podjetje bo kombinacija izložkov na MPM, ki je najbolj dobičkonosna.[2]
Z vidika makroekonomije MPM ponazarja proizvodne možnosti, ki so na voljo državi ali gospodarstvu v določenem časovnem obdobju za široke kategorije proizvodnje. Tradicionalno se uporablja za prikaz gibanja med namenjanjem vseh sredstev potrošnji na osi »y« in naložbami na osi »x«. Vendar lahko gospodarstvo doseže proizvodno učinkovitost, ne da bi bilo nujno alokativno učinkovito. Nedelovanje trga (na primer nepopolna konkurenca ali zunanji učinki) in nekatere institucije družbenega odločanja (na primer vlada in tradicija) lahko povzročijo, da se proizvaja napačna kombinacija dobrin (zato se viri dodelijo proizvodnjama obeh dobrin napačno) v primerjavi s tem, kar bi potrošniki raje imeli glede na to, kaj je izvedljivo na MPM.[3]
Sklici
[uredi | uredi kodo]- ↑ Sickles, R., & Zelenyuk, V. (2019). Measurement of Productivity and Efficiency: Theory and Practice. Cambridge: Cambridge University Press. doi:10.1017/9781139565981
- ↑ Coelli, Time; Prasada Rao, D. S.; Battese, George E. (1998). An Introduction to Efficiency and Productivity Analysis. Springer. str. 59–60. ISBN 978-0-7923-8062-7.
- ↑ Farrell, M. J. (1957). »The Measurement of Productive Efficiency«. Journal of the Royal Statistical Society. Journal of the Royal Statistical Society. Series A (General), Vol. 120, No. 3. 120 (3): 253–290. doi:10.2307/2343100. JSTOR 2343100.
