Delaunayeva triangulacija
Delaunayeva triangulacija se imenuje po ruskem matematiku Borisu Nikolajeviču Delaunayu, ki jo je izumil leta 1934. Triangulacija je Delaunayeva, če izpolnjuje Delaunayev pogoj, ki pravi, da v nobenem krogu, ki bi bil očrtan nekemu trikotniku triangulacije, ne sme biti nobena točka. S tem se dobi triangulacijo, ki ima najmanjše število tankih trikotnikov (trikotnikov z majhnimi notranjimi koti), kar je nezaželeno in povzroča nevšečnosti v praksi.
Potek triangulacije
[uredi | uredi kodo]-
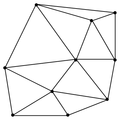
Slika 1. Naključne točke
-
Slika 2. Triangulacija
-
Slika. 3. Pregled ali izpolnjuje Delaunayev pogoj
Algoritmi
[uredi | uredi kodo]Naključni inkrementalni algoritem
[uredi | uredi kodo]Algoritmi iz te skupine so najpogosteje uporabljeni. V najslabšem primeru lahko imajo časovno zahtevnost O(N2), vendar je pričakovana časovna zahtevnost O(n log n). Obstaja več rešitev kot je na primer iskalni algoritem, ki v vsakem koraku dodaja po en pravilni trikotnik k trenutni triangulaciji in algoritem z vstavljanjem, ki zaporedoma vstavlja točke v narejeno triangulacijo, nato pa jo popravi, da zadošča Delaunayevemu pogoju.
Algoritem deli in vladaj
[uredi | uredi kodo]Algoritem na začetku množico vhodnih točk razdeli na manjše množice točk, nad katerimi naredi triangulacijo, nato pa te manjše množice združi in naredi celotno triangulacijo.
Algoritem s prebirno premico
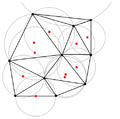
[uredi | uredi kodo]Priljubljeni algoritem s prebirno premico je predlagal Steven Fortune (1987). V bistvu je Fortune razvil algoritem, ki skonstruira dualni graf Delaunayeve triangulacije – Voronojevih diagramov. Časovna zahtevnost je O(n log n).
-
Poišče se središča očrtanih krogov
-
Dobljene točke se poveže in tako nastane Voronojev diagram