Uniformni politop
Uniformni politop je politop, ki ga sestavljajo facete z nižjo razsežnostjo. Uniformni politopi z razsežnostjo 2 so pravilni mnogokotniki. To je posplošitev starejše kategorije polpravilnih politopov, vsebuje pa tudi pravilne politope
Operacije[uredi | uredi kodo]
Skoraj vsak uniformni politop se lahko naredi s pomočjo Wythoffove konstrukcije in se prikaže s Coxeter-Dinkinovim diagramom. Pomembnejše izjeme vključujejo veliko antiprizmo v štirih razsežnostih. Izraz je za konveksne uniformne politope skoval ameriški matematik Norman Johnson (rojen 1930).
Operatorji rektifikacije[uredi | uredi kodo]
Pravilni n-politop ima n-ti red rektifikacije. Ničelna rektifikacija nam da začetno obliko. -ta rektifikacija je dualna. Prva rektifikacija spremeni robove v oglišča, druga rektifikacija spremeni stranske ploskve v oglišča. Tretja rektifikacija spremeni celice v oglišča.
Razširjeni Schläflijev simbol se lahko uporabi za predstavitev rektificiranih oblik z
- k-ta rektifikacija = tk{p1, p2, ..., pn-1}
Operatorji prisekanosti[uredi | uredi kodo]
- t0,1 ali t: prisekanost se lahko uporabi za mnogokotnike in telesa z višjo razsežnostjo. Prisekanost odstrani oglišča in vnese nove facete tja, kjer je prej bilo oglišče. Stranske ploskve so prirezane in robovi podvojeni. Izraz je skoval Johannes Kepler (1671 – 1630). Beseda izhaja iz latinske besede truncare, kar pomeni odrezati.
- t0,2 ali rr: kantelacija se lahko uporabi za poliedre in telesa višjih razsežnosti. Kantelacija odreže oglišča in robove ter jih nadomesti z novimi facetami. Celice se nadomestijo s topološko razširjenimi kopijami. Izraz je skoval matematik Norman Johnson (rojen 1930). Izraz izhaja iz besede cant, ki pomeni nagnjeno ali poševno odrezano.
- t0,2: runcinacija se lahko uporabi za polihorone in telesa z višjimi razsežnostmi. Izraz je skoval Johnson. Izraz izhaja iz besede runcina, ki pomeni tesarski oblič.
- t0,4 ali 2r2r: sterikacija se uporablja za 5-politope in višje razsežnosti. Sterikacija odreže oglišča, robove, stranske ploskve in celice in vse nadomesti z novimi facetami. 5-stranske ploskve zamenja z njihovimi razširjenimi kopijami. Tudi ta izraz je skoval matematik Norman Johnson. Izraz izhaja iz grške besede stereos, ki pomeni trdno telo.
- t0,5: pentelacija se uporablja za 6-politope in višje razsežnosti. Pentelacija odreže oglišča, robove, stranske ploskve, celice in 4-stranske ploskve ter jih nadomesti z novimi facetami. 6-stranske ploskve nadomesti s topološko razširjenimi kopijami. Izraz izhaja iz grške besede penta, kar pomeni pet.
- t0,6 ali 3r3r: heksikacija se uporablja za 7-politope in višje razsežnosti. Heksikacija odreže oglišča, robove, stranske ploskve, celice, 4-stranske ploskve, 5-stranske ploskve in 6-stranske ploskve in jih nadomesti z novimi facetami. Izraz izhaja iz grške besede hex, kar pomeni šest.
- t0,7: heptelacija se uporablja za 8-politope in višje razsežnosti. Heptelacija odreže oglišča, robove, stranske ploskve celice, 4-stranske ploskve, 5-stranske ploskve, 6-stranske ploskve in jih zamenja z novimi facetami. 7-stranske ploskve se nadomestijo s topološko razširjenimi kopijami. Izraz izhaja iz grške besede hepta, kar pomeni sedem.
- t0,8 ali 4r4r: oktelacija se uporablja za uniformne 9-politope in višje razsežnosti.
- t0,9: enekacija se uporablja za uniformne 10-politope in višje razsežnosti.
Povečevanje[uredi | uredi kodo]
Znan je še poseben postopek, ki se imenuje alternacija. Ta postopek izmenoma odstrani vsako drugo oglišče v politopu, ki ima samo parne stranske ploskve. Alternirani omniprisekani politop se imenuje prirezani politop.
Vedno lahko konstruiramo takšen politop

Alternacija velikega kubooktaedra naredi prirezano kocko (snub kocka).
Slika oglišč[uredi | uredi kodo]
Uniformni politopi selahko konstruirajo iz njihovih slik oglišč, ki predstavljajo razporeditev robov, stranskih ploskev, celic itd. okoli vsakega oglišča. Uniformni politopi predstavljeni s Coxeter-Dinkinovimi diagrami označujejo aktivna zrcala z obroči imajo zrcalno simetrijo in jih lahko konstruiramo z rekurzivnim zrcaljenjem slike oglišč.
Manjše število nezrcalnih uniformnih politopov ima samo eno sliko oglišč toda se ne ponavljajo s samo enim enostavnim zrcaljenjem slike oglišč.
Uniformni politopi po razsežnostih[uredi | uredi kodo]
Ena razsežnost[uredi | uredi kodo]
Edini enorazsežni politop je del premice (ravne črte). Pripada Coxeterjevi družini A1
Dve razsežnosti[uredi | uredi kodo]
V dveh razsežnostih je neskončno velika skupina konveksnih uniformnih politopov to so pravilni mnogokotniki od katerih je najenostavnejši enakostranični trikotnik. Nekaj prvih pravilnih mnogokotnikov je prikazanih v naslednji preglednici:
| ima | trikotnik (2-simpleks) |
kvadrat (2-ortopleks) (2-kocka) |
petkotnik | šestkotnik | sedemkotnik | osemkotnik |
|---|---|---|---|---|---|---|
| Schläflijev | {3} | {4} | {5} | {6} | {7} | {8} |
| Dinkin | ||||||
| slika | 
|

|

|

|

|

|
Znana je tudi neskončna množica zvezdnih mnogokotnikov (eden za vsako racionalno število večje od 2), toda ti niso konveksni. Najenostavnejši primer je pentagram, ki odgovarja racionalnemu številu 5/2.
| ime | pentagrami | heptagrami | oktagram | eneagrami | dekagram | ...n-agrami | ||
|---|---|---|---|---|---|---|---|---|
| Schläfli | {5/2} | {7/2} | {7/3} | {8/3} | {9/2} | {9/4} | {10/3} | {p/q} |
| Dinkin | ||||||||
| slika | 
|

|

|

|

|

|

|
|
Tri razsežnosti[uredi | uredi kodo]
V treh razsežnostih postane vse še bolj zanimivo. Obstaja pet pravilnih poliedrov, ki so znani kot platonska telesa:
| Name | Schläfli {p,q} |
Dinkin |
Slika (prosojna) |
Slika (telo) |
Slika (krogla) |
stranske ploskve {p} |
robovi | oglišča {q} |
simetrija | dualni |
|---|---|---|---|---|---|---|---|---|---|---|
| tetraeder (3-simpleks) (piramida) |
{3,3} | 
|

|

|
4 {3} |
6 | 4 {3} |
Td | (self) | |
| kocka (3-kocka) (heksaeder) |
{4,3} | 
|

|

|
6 {4} |
12 | 8 {3} |
Oh | Octahedron | |
| oktaeder (3-ortopleks) |
{3,4} | 
|

|

|
8 {3} |
12 | 6 {4} |
Oh | Cube | |
| dodekaeder | {5,3} | 
|

|

|
12 {5} |
30 | 20 {3}2 |
Ih | ikozaeder | |
| ikozaeder | {3,5} | 
|

|

|
20 {3} |
30 | 12 {5} |
Ih | dodekaeder |
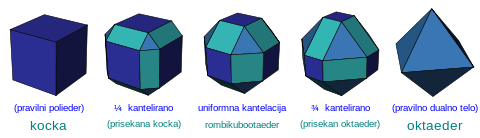
Dodatno k tem telesom je znanih še 13 polpravilnih poliedrov, ki so znani kot arhimedska telesa. Dobi se jih s pomočjo Wythoffove konstrukcije ali z uporabo postopkov kot je prisekavanje platonskih teles, kar je prikazano v naslednji preglednici:
| osnovno telo | prisekano | rektificirano | dvojno prisekano | dvojno rektificirano (dualno) |
Kantelirano | omniprisekano (kantiprisekano) |
Prirezana oblika | |
|---|---|---|---|---|---|---|---|---|
| tetraedrska 3-3-2 |
 {3,3} |
 (3.6.6) |
 (3.3.3.3) |
 (3.6.6) |
 {3,3} |
 (3.4.3.4) |
 (4.6.6) |
 (3.3.3.3.3) |
| Octahedral 4-3-2 |
 {4,3} |
 (3.8.8) |
 (3.4.3.4) |
 (4.6.6) |
 {3,4} |
 (3.4.4.4) |
 (4.6.8) |
 (3.3.3.3.4) |
| Icosahedral 5-3-2 |
 {5,3} |
 (3.10.10) |
 (3.5.3.5) |
 (5.6.6) |
 {3,5} |
 (3.4.5.4) |
 (4.6.10) |
 (3.3.3.3.5) |
Obstaja tudi neskončna množica prizem, po ena za vsak pravilni mnogokotnik ter pripadajoča množica antiprizem.
| # | Name | Picture | Tiling | Vertex figure |
Coxeter-Dinkin and Schläfli symbols |
|---|---|---|---|---|---|
| P2p | prizma | 
|

|

|
t{2,p} |
| Ap | antiprizma | 
|

|

|
t{2,p} |
Nekonveksni uniformni poliedri vključujejo še 4 pravilne poliedre, ki jih poznamo kot Kepler-Poinsotovi poliedri ter 53 polpravilnih nekonveksnih poliedrov. Obstajata tudi dve neskončni množici zvezdnih prizem (po ena za vsak zvezdni mnogokotnik) ter zvezdne antiprizme (po ena za vsako racionalno število večje od 3/2).
Konstrukcije[uredi | uredi kodo]
Wythoffove uniformne poliedre in tlakovanja lahko definiramo z uporabo Wythoffovega simbola, ki določa osnovno področje objekta. Razširitev Schläflijeve notacije se lahko uporabi za vse razsežnosti.
| postopek | razširjeni Schläflijevi simboli |
Coxeter- Dinkinov diagram |
Wythoff symbol |
Položaj | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (2) | (1) | (0) | (0,1) | (0,2) | (1,2) | ||||||
| starševska | t0{p,q} | q | 2 p | {p} | {} | -- | -- | -- | {} | |||
| rektificirano | t1{p,q} | 2 | p q | {p} | -- | {q} | -- | {} | -- | |||
| dvojno rektificirano (or dualni) |
t2{p,q} | p | 2 q | -- | {} | {q} | {} | -- | -- | |||
| prisekan | t0,1{p,q} | 2 q | p | {2p} | {} | {q} | -- | {} | {} | |||
| dvojno prisekan (ali prisekan dual) |
t1,2{p,q} | 2 p | q | {p} | {} | {2q} | {} | {} | -- | |||
| kantelirano (ali razširjeno) |
t0,2{p,q} | p q | 2 | {p} | {}x{} | {q} | {} | -- | {} | |||
| kantiprisekano (ali omniprisekano) |
t0,1,2{p,q} | 2 p q | | {2p} | {}x{} | {2q} | {} | {} | {} | |||
| prisekan | s{p,q} | | 2 p q | {p} | {3} {3} |
{q} | -- | -- | -- | |||

|
 generiranje trikotnikov |
Štiri razsežnosti[uredi | uredi kodo]
V štirih razsežnostih obstaja 6 konveksnih pravilnih polihoronov, 17 prizem zgrajenih na platonskih in arhimedskih telesih in dve neskončni množici prizem in konveksnih antiprizem ter duoprizem. Razen tega imamo še 41 konveksnih polpravilnih polihoronov vključno z neWythoffovimi velikimi antiprizmami in prirezanimi 24-celicami. Obe skupini od teh posebnih polihoronov sta sestavljeni iz podgrup oglišč 600-celic.
Štirirazsežni nekonveksni uniformni politopi so prešteti. Vključujejo 10 pravilnih nekonveksnih polihoronov ( Schläfli-Hessovi polihoroni) in 57 prizem osnovanih na nekonveksnih uniformnih poliedrih ter tri neskončne skupine zvezdnih prizem osnovanih na zvezdnih antiprizmah, duoprizme nastale kot množenje dveh zvezdnih mnogokotnikov in duoprizme, ki nastanejo z množenjem običajnih mnogokotnikov z zvezdnimi mnogokotniki. Obstaja tudi neznano število polihoronov, ki ne spadajo v zgornje skupine. Preko tisoč so jih doslej našli.

Nas liki so trije pravi diederski koti, od katerih dva sekata pravokotni zrcali:
robovi 1 do 2, 0 do 2 in 1 do 3.

Prisekane oblike[uredi | uredi kodo]
V naslednji preglednici je definiranih 15 oblik. Vsako prisekanje tvori obliko iz ene ali štirih rst celic, ki se nahajajo na mestih označenih z 0, 1, 2, 3 kot je to označeno zgoraj. Celice so označene z oznakami za prisekovanje:
- n-kotna prizma je prikazana kot {n}x{2}.
- zeleno ozadje je prikazano na oblikah, ki so enakovredne osnovni ali dualni obliki
rdeče ozadje prikazuje prisekanja osnovnih oblik in modro prisekanja dualnih oblik
| operacija | razširjeni Schläflijevi simboli |
Coxeter- Dinkinov diagram |
položaj | |||
|---|---|---|---|---|---|---|
| (3) | (2) | (1) | (0) | |||
| starševski | t0{p,q,r} | {p,q} |
{p} |
{} |
-- | |
| rektificirano | t1{p,q,r} | t1{p,q} |
{p} |
-- |
{q,r} | |
| dvojno rektificirano (ali rektificirani dual) |
t2{p,q,r} | {q,p} |
-- |
{r} |
t1{q,r} | |
| trojno rektificirano (ali dual) |
t3{p,q,r} | -- |
{} |
{r} |
t2{q,r} | |
| prisekano | t0,1{p,q,r} | t0,1{p,q} |
{2p} |
{} |
{q,r} | |
| dvojna prisekanost | t1,2{p,q,r} | t1,2{p,q} |
{p} |
{r} |
t0,1{q,r} | |
| trojna prisekanost (ali prisekani dual) |
t2,3{p,q,r} | {q,p} |
{} |
{2r} |
t1,2{q,r} | |
| kantelirano | t0,2{p,q,r} | t0,2{p,q} |
{p} |
{}x{r} |
t1{q,r} | |
| dvojno kantelirano (ali kantelirani dual) |
t1,3{p,q,r} | t1{p,q} |
{p}x{} |
{r} |
t0,2{q,r} | |
| runcinirano (ali razširjeno) |
t0,3{p,q,r} | {p,q} |
{p}x{} |
{}x{r} |
t2{q,r} | |
| kaniprisekano | t0,1,2{p,q,r} | t0,1,2{p,q} |
{2p} |
{}x{r} |
t0,1{q,r} | |
| dvojno kantiprisekano (ali kantiprisekani dual) |
t1,2,3{p,q,r} | t1,2{p,q} |
{p}x{} |
{2r} |
t0,1,2{q,r} | |
| runciprisekano | t0,1,3{p,q,r} | t0,1{p,q} |
{2p}x{} |
{}x{r} |
t0,2{q,r} | |
| runcikantelirano (ali runciprisekani dual) |
t0,2,3{p,q,r} | t0,1,2{p,q} |
{p}x{} |
{}x{2r} |
t1,2{q,r} | |
| runciprisekano (ali omniprisekano) |
t0,1,2,3{p,q,r} | t0,1,2{p,q} |
{2p}x{} |
{}x{2r} |
t0,1,2{q,r} | |
Pet in več razsežnosti[uredi | uredi kodo]
V peti in višjih razsežnostih so znani trije pravilni politopi. To so hiperkocka, simpleks in ortopleks (kokocka), ki so posplošitve trirazsežnih teles (kocke, tetraedra in oktaedra). V treh razsežnostih ni pravilnih zvezdnih politopov. Večino večrazsežnih politopov se dobi s spremembami pravilnih pravilnih politopov ali s pomočjo kartezičnega produkta politopov z nižjimi razsežnostmi.
Zunanje povezave[uredi | uredi kodo]
- Uniformni politop v Glossary for Hyperspace (angleško)
- Uniformni politopi v štirih razsežnostih (nemško)