Seznam fraktalov po Hausdorff-Bezikovičevi razsežnosti

Fraktal je geometrijski objekt, katerega Hausdorff-Bezikovičeva razsežnost (δ) strogo presega svojo topološko razsežnost. Tu je predstavljeno nekaj fraktalov, razvrščenih po naraščajoči Hausdorff-Bezikovičevi razsežnosti z namenom ponazoritve kaj pomeni da ima fraktal majhno ali veliko razsežnost.

Deterministični fraktali

δ (točna vrednost)	δ (vrednost)	ime	prikaz	opombe
$\textstyle {{\frac {\ln(2)}{\ln(\delta )}}?}$	0.4498?	bifurkacije logistične preslikave		V bifurkacijskem grafu se pri približevanju kaotičnega področja pojavijo zaporedne podvojitve period, kjer geometrično zaporedje teži k 1/δ. (δ=4,6692, prva Feigenbaumova konstanta).
$\textstyle {\frac {\ln(2)}{\ln(3)}}$	0.6309	Cantorjeva množica		Ustvarjena z odstranjevanjem tretjine v vsaki ponovitvi. Nikjer gosta in neštevna množica.
$\log {(1+{\sqrt {2}})}$	0.88137	spekter Fibonaccijevega hamiltonskega sistema		Spekter konvergira k eksplicitni konstanti.
$\textstyle {1}$	1	Smith-Volterra-Cantorjeva množica		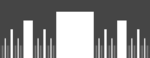Ustvarjena z odstranitvijo sredinskega intervala dolžine 1/2^{2n} za vsak preostal interval n-te ponovitve. Nikjer gosta množica, a z Lebesguovo mero ½.
$\textstyle {\frac {\ln(8)}{\ln(7)}}$	1.0686	obris Gosperjevega otoka
izmerjeno (škatlično štetje)	1.2	vejasta Juliajeva množica		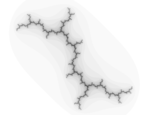Juliajeva množica s parametroma: Realni del=0 in Imaginarni del=1.
$\textstyle {3{\frac {\log(\phi )}{\log({\frac {3+{\sqrt {13}}}{2}})}}}$	1.2083	Fibonaccijev fraktal 60°		Ustvarjena iz Fibonaccijeve besede. Glej tudi standardni Fibonaccijev fraktal.
	1.26	Hénonova preslikava		Kanonična Hénonova preslikava s parametroma a = 1,4 in b = 0,3 ima Hausdorff-Bezikovičevo razsežnost δ = 1,261 ± 0,003. Različni parametri dajo različne vrednosti δ.
$\textstyle {\frac {\ln(4)}{\ln(3)}}$	1.2619	Kochova krivulja		Tri von Kochove krivulje tvorijo Kochovo snežinko, oziroma antisnežinko.
$\textstyle {\frac {\ln(4)}{\ln(3)}}$	1.2619	obris trojne zmajeve krivulje		L-sistem: enak kot zmajeva krivulja s kotom =30°. The Fudgeflake (zmečkana snežinka) temelji na 3 začetnih točkah, postavljenih v trikotnik.
$\textstyle {\frac {\ln(4)}{\ln(3)}}$	1.2619	dvorazsežni Cantorjev prah		Dvorazsežna Cantorjeva množica.
izračunano	1.2683	Juliajeva množica z²-1		Juliajeva množica za c=-1.
	1.3057	Apolonijeva mreža		Tudi »Apolonijevo tesnilo«.
izračunano	1.3934	Douadyjev zajec		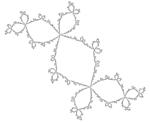Juliajeva množica za c=-0,123+0.745i.
$\textstyle {\frac {\ln(5)}{\ln(3)}}$	1.4649	škatelni fraktal		Ustvarjena z izmenjajočim ponavljanjem kvadratov križa iz petih kvadrat(k)ov.
$\textstyle {\frac {\ln(5)}{\ln(3)}}$	1.4649	kvadratna Kochova krivulja (tip 1)		Vzorec škatelnega fraktala (zgoraj).
$\textstyle {\frac {\ln(8)}{\ln(4)}}$	1.5000	kvadratna Kochova krivulja (tip 2)		Imenovana tudi »klobasa Minkovskega«.
	1.5236	obris zmajeve krivulje		Cf Chang & Zhang.
$\textstyle {\frac {\ln(3)}{\ln(2)}}$	1.5850	trovejno drevo		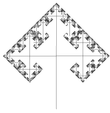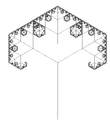Vsaka veja drži 3 veje. (tukaj 90° in 60°). Razsežnost fraktala celotnega drevesa je fraktalna razsežnost zadnje veje. Toda: drevo z dvema vejama ima fraktalno razsežnost 1.
$\textstyle {\frac {\ln(3)}{\ln(2)}}$	1.5850	trikotnik Sierpinskega		Tudi Pascalov trikotnik modulo 2.
$\textstyle {\frac {\ln(3)}{\ln(2)}}$	1.5850	puščična krivulja Sierpinskega		Ustvarjena z enorazsežno krivuljo.
$\textstyle {1+{\frac {\ln 2}{\ln 3}}}$	1.6309	Pascalov trikotnik modulo 3		Za trikotnik modulo k, kjer je k praštevilo, je fraktalna razsežnost $\scriptstyle {1+log_{k}({\frac {k+1}{2}})}$(Cf Stephen Wolfram)
$\textstyle {3{\frac {\log(\phi )}{\log(1+{\sqrt {2}})}}}$	1.6379	Fibonaccijev fraktal		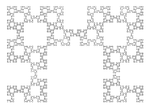Fraktal iz Fibonaccijeve besede (OEIS A005614). Ilustracija: fraktal po F23 (28657) korakih. .
$\textstyle {1+{\frac {\ln 3}{\ln 5}}}$	1.6826	Pascalov trikotnik modulo 5		Za trikotnik modulo k, kjer je k praštevilo, je fraktalna razsežnost $\scriptstyle {1+log_{k}({\frac {k+1}{2}})}$ (Cf Stephen Wolfram)
$\textstyle {\frac {\log(4)}{\log({\sqrt {5}})}}$	1.7227	vetrnični fraktal		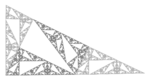Grajen na podlagi Conway-Radinovega vetrničnega pokritja.
$\textstyle {\frac {\ln(7)}{\ln(3)}}$	1.7712	snežinka šestkotnikov		Ustvarjena z izmenjujočim ponavljanjem 7 šestkotnikov. Njena meja je Kochova snežinka. Vsebuje neskončno Kochovih snežink.
log(7) / log(3)	1.7712	Fractal H-I de Rivera
$\textstyle {\frac {ln(4)}{ln(2(1+cos(85^{\circ }))}}$	1.7848	Kochova krivulja 85°, Cesarejev fraktal		Izhaja iz Kochove krivulje s kotom med 0 in 90°. Fraktalna razsežnost: $\scriptstyle {\frac {ln(4)}{ln(2(1+cos(a))}}$. Cesarejev fraktal izhaja iz tega vzorca.
$\textstyle {\frac {\ln(6)}{\ln(1+\phi )}}$	1.8617	snežinka petkotnikov		Ustvarjena z izmenjujočim ponavljanjem 6 petkotnikov. $\phi$ = zlati rez = $\scriptstyle {\frac {1+{\sqrt {5}}}{2}}$
$\textstyle {\frac {\ln(8)}{\ln(3)}}$	1.8928	preproga Sierpinskega
$\textstyle {\frac {\ln(8)}{\ln(3)}}$	1.8928	trirazsežni Cantorjev prah		Trorazsežna Cantorjeva množica.
$\textstyle {{\frac {\ln(4)}{\ln(3)}}+{\frac {\ln(2)}{\ln(3)}}={\frac {\ln(8)}{\ln(3)}}}$	1,8928	kartezični produkt Kochove krivulje in Cantorjeve množice		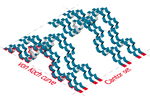Posplošitev: Naj je F×G kartezični produkt dve fraktalnih množic F ind G. Potem velja $Dim_{H}(FxG)=Dim_{H}(F)+Dim_{H}(G)$.. Glej tudi dvorazsežni Cantorjev prah in Cantorjeva kocka.
ocenjeno	1.9340	obris Lévyjeve C-krivulje		Ocena Duvalla in Keeslinga (1999). Krivulja ima fraktalno razsežnost 2.
	1.974	Penroseovo pokritje		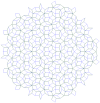See Ramachandrarao, Sinha & Sanyal
$\textstyle {2}$	2	Mandelbrotova množica		Vsaka ravnina predmeta, ki vsebuje disk, ima Hausdorff-Bezikovičevo razsežnost δ = 2. Toda tudi meja Mandelbrotove množice ima tudi Hausdorff-Bezikovičevo razsežnost δ = 2.
$\textstyle {2}$	2	Juliajeva množica		za določene vrednosti c (vključno s c na meji Mandelbrotove množice), ima Juliajeva množica fraktalno razsežnosz 2. .
$\textstyle {2}$	2	krivulja Sierpinskega		Vsaka Peanova krivulja, ki zapolni ravnino, ima Hausdorff-Bezikovičevo razsežnost δ = 2.
$\textstyle {2}$	2	Hilbertova krivulja		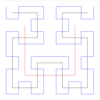Na podoben način: Moorova krivulja. Se lahko razširi v tri razsežnosti.
$\textstyle {2}$	2	Peanova krivulja		Družina krivulj, ustvarjeni na podoben način, kot npr. Wunderlichove krivulje.
$\textstyle {2}$	2	Moorova krivulja		Se lahko razširi v tri razsežnosti.
	2	Lebesguova krivulja ali krivulja reda z		Drugače kot prejšnje je ta krivulja, ki lahko zapolni prostor, odvedljiva praktično povsod. Prav tak tip krivulje lahko določimo v dveh razsežnostih. Kot Hilbertova krivulja se lahko razširi v tri razsežnosti.
$\textstyle {\frac {ln(2)}{ln({\sqrt {2}})}}$	2	zmajeva krivulja		Njene meje imajo fraktalno razsežnost 1.5236.
	2	trojna zmajeva krivulja		L-System: F-> F+F-F. kot=120°.
$\textstyle {\frac {ln(4)}{ln(2)}}$	2	T-kvadrat
$\textstyle {\frac {ln(4)}{ln(2)}}$	2	Gosperjeva krivulja		Njena meja je Gosperjev otok.
$\textstyle {\frac {ln(4)}{ln(2)}}$	2	tetraeder Sierpinskega		Vsak tetraeder nadomestimo s 4 tetraedri.
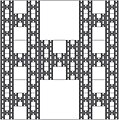
$\textstyle {\frac {ln(4)}{ln(2)}}$	2	H-drevo		Tudi »H-fraktal« in »Mandelbrotovo drevo«, ki ima enak vzorec.
$\textstyle {{\frac {\log(2)}{\log(2/{\sqrt {2}})}}=2}$	2	Pitagorovo drevo		Vsak kvadrat generira 2 kvadrata, pomanjšana za faktor ${\sqrt {2}}/2$.
$\textstyle {\frac {ln(4)}{ln(2)}}$	2	dvorazsežni grški križ		Vsak del nadomestimo s kržem iz 4 delov.
	2.06	Lorenzev atraktor		Za točne vrednosti parametrov.
$\textstyle {\frac {ln(20)}{ln(2+\phi )}}$	2.3296	dodekaederski fraktal		Vsak dodekakeder (dvanajsterec, pravilno telo, ki ga omejuje 12 pravilnih peterokotnikov) nadomestimo z 20 dodekaedri.
$\textstyle {\frac {ln(13)}{ln(3)}}$	2.3347	trirazsežna kvadradna Kochova ploskev (tipa 1)		Razširitev kvadratne Kochove krivulje tipa 1 v tri razsežnosti. Slika prikazuje drugo ponovitev.
	2.4739	Apollonijevo pakiranje krogel		The interstice left by the apollolian spheres. Apollonian gasket in 3D. Dimension calculated by M. Borkovec, W. De Paris, and R. Peikert.
$\textstyle {\frac {ln(32)}{ln(4)}}$	2.50	trirazsežna Kochova ploskev (tipa 2)		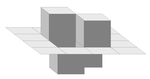Razširitev kvadratne Kochove krivulje (tipa 2) v tri razsežnosti. Slika prikazuje prvo ponovitev.
$\textstyle {\frac {ln(16)}{ln(3)}}$	2.5237	Cantorjev teserakt		Cantorejeva množica v štirih razsežnostih. Posplošitev: v prostoru z razsežnostjo n, ima Cantorjeva množica Hausdorff-Bezikovičevo razsežnost $\scriptstyle {n{\frac {ln(2)}{ln(3)}}}$
$\textstyle {\frac {ln(12)}{ln(1+\phi )}}$	2.5819	ikozaedrski fraktal		Vsak ikozaeder nadomestimo z 12 ikozaedri.
$\textstyle {\frac {ln(6)}{ln(2)}}$	2.5849	trirazsežni grški križ		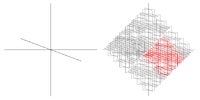Each segment is replaced by a cross formed by 6 segments.
$\textstyle {\frac {ln(6)}{ln(2)}}$	2.5849	oktaedrski fraktal		Vsak oktaeder nadomestimo s 6 oktaedri.
$\textstyle {\frac {\log(6)}{\log(2)}}$	2.5849	Kochova ploskev		vsak enakostranični trikotnik zamenjamo s 6 dvakrat manjšimi trikotniki.
$\textstyle {\frac {ln(20)}{ln(3)}}$	2.7268	Mengerjeva spužva		Njena površina ima fraktalno razsežnost $\scriptstyle {{\frac {ln(12)}{ln(3)}}=2.2618}$.
$\textstyle {\frac {ln(8)}{ln(2)}}$	3	trirazsežna Hilbertova krivulja		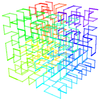Hilbertova krivulja razširjena v tri razsežnosti.
$\textstyle {\frac {ln(8)}{ln(2)}}$	3	trirazsežna Lebesguova krivulja		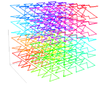Lebesguova krivulja razširjena v tri razsežnosti.
$\textstyle {{\frac {\log(8)}{\log(2)}}=3}$	3	trirazsežna Moorova krivulja		Moorova krivulja razširjena v tri razsežnosti.

Naključni in naravni fraktali

δ (točna vrednost)	δ (vrednost)	ime	prikaz	opombe
izmerjeno	1.22 ± 0.02	obris obale Irske		Vrednosti fraktalne razsežnosti celotne irske obale so določili McCartney, Abernethy in Gault na Univerzi Ulstra in študentje teoretične fizike na Kolidžu Trinity v Dublinu pod vodstvom S. Hutzlerja. Med neravno zahodno obalo (fraktalna razsežnost je približno 1,26) in veliko gladkejšo vzhodno obalo (fraktalna razsežnost je 1,10) je precejšnja razlika.
izmerjeno	1.24	obris obale Velike Britanije
$\textstyle {\frac {4}{3}}$	1.33	obris Brownovega gibanja		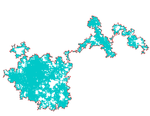(Cf Wendelin Werner).
$\textstyle {\frac {4}{3}}$	1.33	dvorazsežni polimer		Similar to the brownian motion in 2D with non self-intersection.
$\textstyle {\frac {4}{3}}$	1.33	Percolation front in 2D, Corrosion front in 2D		Fractal dimension of the percolation-by-invasion front, at the percolation threshold (59.3%). It’s also the fractal dimension of a stopped corrosion front.
	1.40	Clusters of clusters 2D		When limited by diffusion, clusters combine progressively to a unique cluster of dimension 1.4.
izmerjeno	1.52	obris obale Norveške
izmerjeno	1.55	naključni sprehod brez sekanj		Self-avoiding random walk in a square lattice, with a « go-back » routine for avoiding dead ends.
$\textstyle {\frac {5}{3}}$	1.66	trirazsežni polimer		Similar to the brownian motion in a cubic lattice, but without self-intersection.
	1.70	2D DLA Cluster		In 2 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 1.70.
$\textstyle {\frac {91}{48}}$	1.8958	2D Percolation cluster		Under the percolation threshold (59.3%) the percolation-by-invasion cluster has a fractal dimension of 91/48. Beyond that threshold, le cluster is infinite and 91/48 becomes the fractal dimension of the « clearings ».
$\textstyle {\frac {ln(2)}{ln({\sqrt {2}})}}$	2	Brownovo gibanje		Or random walk. The Hausdorff dimensions equals 2 in 2D, in 3D and in all greater dimensions (K.Falconer "The geometry of fractal sets").
izmerjeno	približno 2	porazdelitev galaktičnih jat		Iz rezultatov pregleda SDSS leta 2005.
$\textstyle {\frac {ln(13)}{ln(3)}}$	2.33	površina cvetače		Every branch carries around 13 branches 3 times smaller.
	2.5	klobčiči zmečkanega papirja		When crumpling sheets of different sizes but made of the same type of paper and with the same aspect ratio (for example, different sizes in the ISO 216 A series), then the diameter of the balls so obtained elevated to a non-integer exponent between 2 and 3 will be approximately proportional to the area of the sheets from which the balls have been made. [1] Arhivirano 2010-06-28 na Wayback Machine. Creases will form at all size scales (see Universality (dynamical systems)).
	2.50	Lichtenbergova figura		In 3 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 2.50.
$\textstyle {3-{\frac {1}{2}}}$	2.5	pravilna Brownova ploskev		.
	2.50	3D DLA Cluster		In 3 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 2.50.
izmerjeno	2.52	trirazsežni ponikalni oblak
izmerjeno	2.66	brstnati ohrovt
	2.79	površina skorje človeških možgan
	2.97	površina človeških pljuč		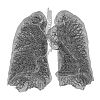The alveoli of a lung form a fractal surface close to 3.
izračunano	3	kvantna struna, ki se kopiči naključno		Hausdorff-Bezikovičeva razsežnost kvantne strune, katere reprezentativna točka se naključno kopičiti skozi zančni prostor.

Viri

• Barnsley, Michael Fielding (1993). Fractals Everywhere. Morgan Kaufmann. ISBN 0-12-079061-0.
• ¹Falconer, Kenneth (Marec 1990). Fractal Geometry. John Wiley & Son Ltd. ISBN 0-471-92287-0.
• Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd. xxv. ISBN 0-470-84862-6.
• Hutzler, S. (2013). »Fractal Ireland«. Science Spin. Zv. 58. str. 19–20. Arhivirano iz prvotnega spletišča dne 26. julija 2013. Pridobljeno 28. maja 2013.
• Mandelbrot, Benoît B. (september 1982). The Fractal Geometry of Nature. W. H. Freeman & Co. ISBN 0-7167-1186-9.{{navedi knjigo}}: Vzdrževanje CS1: samodejni prevod datuma (povezava)
• McCartney, M.; Abernethy, G.; Gault, L (2010). »The Divider Dimension of the Irish Coast«. Irish Geography. Zv. 43. str. 277–284.
• Peitgen, Heinz-Otto (Avgust 1988). Dietmar Saupe (ur.). The Science of Fractal Images. Springer Verlag. ISBN 0-387-96608-0.
• Sapoval, Bernard (2001). Universalités et fractales. Flammarion-Champs. ISBN 2-080-81466-4.

Glej tudi

• fraktalna razsežnost

Zunanje povezave

• Fraktali na Mathworld (angleško)
• Drugi fraktali na spletni strani Paula Bourkeja Arhivirano 2006-09-05 na Wayback Machine. (angleško)
• Solerjeva galerija (angleško)
• Fraktali na mathcurve.com (angleško)
• 1000fractales.free.fr - Projekt zbiranja fraktalov tvorjenih z različnimi programji (angleško)
• Fractals unleashed (angleško)