Michaelis-Mentenina enačba

Michaelis–Mentenina krivulja prikazuje odvisnost hitrosti reakcije V₀ od koncentracije substrata [S].

Michaelis-Mentenina enačba (znana tudi kot Michaelis-Menten-Henrijeva enačba) je enačba, ki prikazuje odvisnost začetne hitrosti encimsko katalizirane reakcije od koncentracije substrata. V primerjavi s kompleksnejšimi modeli približno opisuje splošno kinetiko mnogih encimov, brez vpliva alosterije in kooperativnosti.

Osnovno enačbo lahko zapišemo kot:

${\begin{aligned}v_{0}&={\frac {v_{\max }\cdot {[}S{]}}{K_{M}+{[}S{]}}}\end{aligned}}$

Legenda:

• $v_{0}$ $[{\frac {mol}{L\cdot s}}]$: začetna hitrost
• $v_{max}$ $[{\frac {mol}{L\cdot s}}]$: maksimalna hitrost
• $[S]$ $[{\frac {mol}{L}}]$: koncentracija substrata
• $K_{M}$ $[{\frac {mol}{L}}]$ : Michaelisova konstanta

Enačba nosi ime po dveh biokemikih, Leonor Michelisu in Maud Mentenovi, ki sta leta 1913 opisala splošno teorijo delovanja encimov in izpeljala matematično enačbo, ki popisuje hiperbolično obliko krivulje in omogoča izračun kinetičnih parametrov.

Izpeljava enačbe

Izpeljava enačbe temelji na spodnji reakcijski shemi in dveh ključnih predpostavkah: celotna koncentracija encima in koncentracija intermediarnega kompleksa se skozi čas ne spreminjata.

$E+S{\overset {k_{1}}{\underset {k_{-1}}{\begin{smallmatrix}\displaystyle \longrightarrow \\\displaystyle \longleftarrow \end{smallmatrix}}}}ES{\overset {k_{2}}{\longrightarrow }}E+P\qquad \qquad (1)$

Po Briggsu in Haldaneju se lahko enačbo izpelje na naslednji način, pri čemer je predpostavljeno, da je encimska reakcija ireverzibilna in da se produkt ne veže na encim v začetku.

Prva ključna predpostavkja je vpeljava psevdostacionarnega stanja, kjer se se koncentracija kompleksa encim-substrat ([ES]) spreminja veliko počasneje kot koncentraciji produkta ([P]) in substrata ([S]). Zaradi tega lahko zapišemo spremembo [ES] kot 0 in nastanek produkta:

${\begin{aligned}{\frac {d{[}ES{]}}{dt}}&=k_{1}{[}E{]}{[}S{]}-{[}ES{]}(k_{-1}+k_{2})\;{\overset {!}{=}}\;0\qquad (2)\\{\frac {d{[}P{]}}{dt}}&=k_{2}{[}ES{]}\qquad (3)\\\end{aligned}}$

Druga ključna predpostavka je, da se celotna (totalna) koncetracija encima ([E]_T) ne spreminja skozi čas, kar pomeni da je ([E]_T) vsota proste (nevezane) koncentracije encima ([E]) in koncentracije encima, vezanega na substrat ([ES]):

${[}E{]}_{T}={[}E{]}+{[}ES{]}\;{\overset {!}{=}}\;{\text{konst}}.$

Z vstavljanjem slednjega v enačbo (2) lahko izrazimo [ES], s čimer lahko v kočni fazi izrazimo začetno hitrost encimsko katalizirane reakcije (3):

${\begin{aligned}0&=k_{1}{[}S{]}({[}E{]}_{T}-{[}ES{]})-{[}ES{]}(k_{-1}+k_{2})\\k_{1}{[}S{]}{[}E{]}_{T}&=k_{1}{[}S{]}{[}ES{]}+{[}ES{]}(k_{-1}+k_{2})\\{[}S{]}{[}E{]}_{T}&={[}S{]}{[}ES{]}+{[}ES{]}\underbrace {\frac {(k_{-1}+k_{2})}{k_{1}}} _{K_{M}}\\{[}S{]}{[}E{]}_{T}&=(K_{M}+{[}S{]}){[}ES{]}\\{[}ES{]}&={\frac {{[}S{]}{[}E{]}_{T}}{K_{M}+{[}S{]}}}\\\\{\frac {d{[}P{]}}{dt}}&=v_{0}=k_{2}{[}ES{]}=\underbrace {k_{2}{[}E{]}_{T}} _{v_{\max }}{\frac {{[}S{]}}{K_{M}+{[}S{]}}}\\v_{0}&={\frac {v_{\max }{[}S{]}}{K_{M}+{[}S{]}}}\;\;\;\;\;\qquad \qquad (4)\\\\{\frac {1}{v_{0}}}&={\frac {K_{M}}{v_{\max }}}\cdot {\frac {1}{{[}S{]}}}+{\frac {1}{v_{\max }}}\qquad (5)\end{aligned}}$

Zaradi spreminjanja koncentracije [S] med potekom reakcije se za poenostavitev privzame V₀ in s tem [S] kot začetno koncetracijo substrata. Enačbo (4) se lahko preuredi v enačbo (5), s čimer se lahko nariše Lineweaver–Burkovo krivuljo ali Hanes–Woolfovo krivuljo in tako lažje razbere konstante iz meritev.

Saturacijska krivulja

Saturacijska krivulja za encim prikazuje odvisnost hitrosti reakcije (aktivnosti encima) od koncentracije substrata.

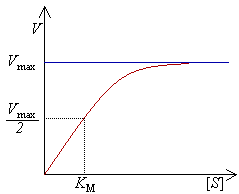
S pomočjo enačbe (4) lahko narišemo t. i. saturacijsko krivuljo (glej graf desno), ki ima obliko hiperbole, in iz katere lahko matematično in grafično razberemo več podatkov:

• Če je $[S]$ večja kot $K_{M}$, velja $[S]/(K_{M}+[S])\approx 1$. Potemtakem je hitrost nastajanja produkta

${\frac {d{[}P{]}}{dt}}\approx v_{\max }=k_{2}[E]_{T}$

V tem primeru je tako hitrost odvisna le od koncentracije encima, in je pomembno le kako hitro kompleks ES pretvori vezan substrat v produkt in ne kako pogosto se encim in substrat srečata v ugodnem položaju za potek reakcije.

• Če je $[S]=K_{M}$, potem je $[S]/(K_{M}+[S])=[S]/(2[S])={\frac {1}{2}}$. Potemtakem je hitrost nastajanja produkta

${\frac {d{[}P{]}}{dt}}=0,5\cdot v_{\max }=0,5\cdot k_{2}[E]_{T}$

• Če je $[S]$ majhna v primerjavi s $K_{M}$, potem velja izraz $[S]/(K_{M}+[S])\approx [S]/K_{M}$ in nastane zelo malo kompleksa ES, zato lahko zapišemo $[E]_{T}\approx [E]$. Potemtakem je hitrost nastajanja produkta

${\frac {d{[}P{]}}{dt}}\approx v_{\max }\cdot [S]/K_{M}\approx {\frac {k_{2}}{K_{M}}}[E][S].$

Hitrost nastajanja produkta je torej odvisna tako od koncentracije encima kot tudi substrata. Reakcija je podobna v tem primeru bimolekularni reakciji s pripadajočo specifično konstanto k₂/K_M. Slednja je merilo za učinkovitost pretvorbe substrata v produkt. Najbolj učinkoviti encimi imajo vrednost k₂/K_M v območju od 10⁸ – 10¹⁰ M⁻¹ s⁻¹, ki je pravzaprav teoretična difuzijska limita v raztopini. Taki encim smatramo za perfektni encim oziroma pravimo, da je encim dosegel katalitično perfekcijo.

Michaelisova konstanta K_M

Hitrost reakcije V pove število reakcij na sekundo, kataliziranih z enim molom encima. Hitrost reakcije narašča s koncentracijo substrata [S], krivulja pa limiti, v tem primeru maksimalni hitrosti V_max, približuje kot asimptota. Zaradi tega ni nobene natančne definirane koncentracije, pri kateri bi bil encim popolnoma nasičen. Mnogo bolj primerno je opisovati kinetične lastnosti encima s pomočjo koncentracije substrata, pri kateri je začetna hitrost reakcije enaka polovici maksimalne vrednosti (V_max/2) in s tem K_M (glej izpeljavo).

Pri encimskih reakcijah, ki delujejo po preprosti Michaelis-Mentenini kinetiki, je konstanta definirana kot:

$K_{M}={\frac {k_{-1}+k_{2}}{k_{1}}}.$

V najpreprostejšem primeru, ko je nastajanje produkta najpočasnejša stopnja, zaradi česar določa končno hitrost (tj. ko je k₂ << k₋₁), bo konstanta enaka disociacijski konstanti ES kompleksa:

$K_{M}\approx {\frac {k_{-1}}{k_{1}}}={\frac {[E][S]}{[ES]}}=K_{d}.$

Pretvorbeno število

Pretvorbeno število v splošnem pove število molov ali molekul substrata, ki se pretvorijo na mol ali molekulo encima v določeni časovni enoti, in je definirano kot:

$k_{3}={\frac {Vmax}{E_{T}}}$ .

Vrednosti pretvorbenega števila za nekatere encime:

Encim	Substrat	k3 (s-1)
katalaza	vodikov peroksid	40.000.000
karboanhidraza	HCO3-	400.000
acetilholin-esteraza	acetilholin	25.000
laktat-dehidrogenaza	laktat	1.000
DNA-polimeraza	DNA	15

Glej tudi

• Lineweaver-Burkova enačba

Viri

• Nelson, D.L.; Cox, M.M. (2008). Lehninger Principles of Biochemistry (5 izd.). NY: W.H. Freeman and Company. COBISS 68330753. ISBN 9781429208925.
• Boyer, R. ([2002] 2005). Temelji biokemije. Ljubljana: Študentska založba, str. 130-134. ISBN 961-242-041-6 (COBISS)

Zunanje povezave

• Splošna izpeljava enačbe (angleško)
• Podrobnejše informacije o encimski kinetiki Arhivirano 2011-08-09 na Wayback Machine. - NIH Chemical Genomics Center (NCGC) (angleško)