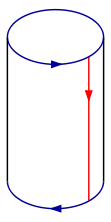
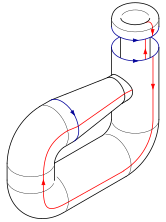
Kleinova steklenica

Kleinova steklenica (tudi Kleinova ploskev) je neorientabilna površina (dvorazsežna mnogoterost). Druga prav tako neorientabilna objekta sta Möbiusov trak in realna projektivna ravnina. Möbiusov trak je površina z mejami, Kleinova steklenica pa nima mej.

Prvi je Kleinovo steklenico opisal v letu 1882 nemški matematik Felix Christian Klein (1849 – 1925). Prvotno so Kleinovo steklenico imenovali Kleinova površina ^[1]

Nastanek[uredi | uredi kodo]

Kleinova steklenica nastane na naslednji način: Pričnemo s kvadratom, ki ga sestavljajo štiri puščice (dve modri in dve rdeči) (korak 1). Zalepimo rdeče in modre puščice in dobimo valj (korak 2). Nato potegnemo konec valja tako, da ga vključimo v začetni valj iz 2. koraka (pri tem seveda nastane presečni krog) (korak 3, 4 in 5). Zaključek valja potegnemo skozi začetni valj (korak 6) in na koncu zavihamo proti začetnemu valju in površino zalepimo z njim. Če bi dodali četrto razsežnost ne bi nastal presečni krog.

1. korak
2. korak
3. korak
4. korak
5. korak
6. korak

Kvadrat imenujemo (je) fundamentalni mnogokotnik za Kleinovo steklenico.

Kleinove steklenice ne moremo realizirati v trirazsežnem prostoru, lahko jo pa v 4-razsežnem. Kleinova steklenica je dvorazsežna mnogoterost, ki obstoja samo v štirih razsežnostih.

Značilnosti[uredi | uredi kodo]

Podobno kot Möbiusov trak je tudi Kleinova steklenica dvorazsežna neorientabilna mnogoterost
V nasprotju z Möbiusovim trakom je Kleinova steklenica zaprta mnogoterost, kar pomeni, da je kompaktna mnogoterost brez mej
Kleinova steklenica se lahko dobi z lepljenjem dveh Möbiusovih trakov
kromatično število je enako 6
neničelna Bettijeva števila so
Kleinova steklenica ne more biti vložena v trirazsežen evklidski prostor, lahko je vanj potopljena
Eulerjeva karakteristika Kleinove steklenice je enaka 0
Kleinove steklenice ne moremo narediti v trirazsežnem prostoru brez sekanja površine, lahko pa jo realiziramo v štirirazsežnem prostoru
prava Kleinova steklenica ne seka svoje površine
Kleinova steklenica nima notranjosti in ima samo eno površino
Kleinove steklenice ne moremo vložiti v trirazsežni prostor, lahko ga pa vanj potopimo
Kleinova steklenica ima takšno površino, da se lahko po njej gibljemo iz zunanjosti v notranjost

Parametrizacija[uredi | uredi kodo]

{\begin{aligned}x&=\left(r+\cos {\frac {u}{2}}\sin v-\sin {\frac {u}{2}}\sin 2v\right)\cos u\\y&=\left(r+\cos {\frac {u}{2}}\sin v-\sin {\frac {u}{2}}\sin 2v\right)\sin u\\z&=\sin {\frac {u}{2}}\sin v+\cos {\frac {u}{2}}\sin 2v\end{aligned}}

.

V parametrični obliki je to

{\begin{aligned}x&={\frac {{\sqrt {2}}f(u)\cos u\cos v(3\cos ^{2}u-1)-2\cos 2u}{80\pi ^{3}g(u)}}-{\frac {3\cos u-3}{4}}\\y&=-{\frac {f(u)\sin v}{60\pi ^{3}}}\\z&=-{\frac {{\sqrt {2}}f(u)\sin u\,\cos v}{15\pi ^{3}g(u)}}+{\frac {\sin u\cos ^{2}u+\sin u}{4}}-{\frac {\sin u\,\cos u}{2}}\end{aligned}}

kjer je

f(u)=20u^{3}-65\pi u^{2}+50\pi ^{2}u-16\pi ^{3}\,

g(u)={\sqrt {8\cos ^{2}2u-\cos 2u(24\cos ^{3}u-8\cos u+15)+6\cos ^{4}u(1-3\sin ^{2}u)+17}}

za 0 ≤ u < 2π in 0 ≤ v < 2π.

V tej parametrizaciji pomeni u pomeni dolžino telesa steklenice, v pa določa njen obseg.

Razdelitev Kleinove steklenice nam da dva Möbiusova trakova.

Razčlenitev[uredi | uredi kodo]

Če razdelimo Kleinovo steklenico vzdolž njene ravnine simetrije dobimo dva zrcalna Möbiusova trakova od katerih je eden nastal tako, kot da bi trak zavrteli v levo, drugi pa v desno.

Kleinovo steklenico lahko naredimo tudi tako, da vzamemo dva Möbiusova trakova in ju zlepimo vzdolž njunih mej. Tako dobimo Kleinovo steklenico v obliki osmice (dobimo jo tudi tako, da zavrtimo osmico okoli osi in jo pri tem pri tem še zavrtimo). To je imerzija (potopitev) Kleinove steklenice. Lahko se dokaže, da je oblika osmice tudi Kleinova steklenica (imenujemo jo tudi podoba 8 Kleinove steklenice). To je samo drugačen model Kleinove steklenice.