Katenoid

Katenoid

Animacija, ki kaže spremembo helikoida v katenoid.

Fizični model katenoida, ki smo ga dobili s pomočjo dveh obročev, potopljenih v milnico. Po dvigu obročev iz milnice obroča počasi razmikamo.

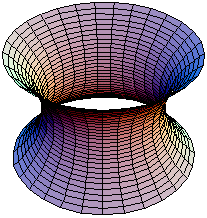
Katenoid (iz latinske besede catena, kar pomeni veriga) je trirazsežna ploskev, ki jo dobimo tako, da zavrtimo verižnico okrog osi z.

Katenoid je prva odkrita minimalna ploskev. Odkril jo je leta 1741 švicarski matematik, fizik in astronom Leonhard Euler (1707 – 1783). Da je katenoid minimalna ploskev, je leta 1776 dokazal tudi Mongeev učenec Jean Baptiste Meusnier. Znani sta samo dve minimalni površini: to sta ravnina in katenoid. Katenoid je tudi edina minimalna površina, ki jo dobimo z vrtenjem neke krivulje.

Katenoid lahko definiramo z naslednjimi tremi parametričnimi enačbami:

$x=c \operatorname {ch} \, \frac{v}{c} \cos u \!\, ,$

$y=c \operatorname {ch} \, \frac{v}{c} \sin u \!\, ,$

$z=v \!\, ,$

kjer je:

• $u \,$ realni parameter
• $v \,$ realni parameter
• $c \,$ neničelna realna konstanta
• $\operatorname {ch} \, (u)$ hiperbolični kosinus
• $\cos (u) \,$ trigonometrična funkcija kosinus
• $\sin (u) \,$ trigonometrična funkcija sinus

V cilindričnih koordinatah je to:

$\rho = c \operatorname {ch} \, \frac{z}{c} \!\, ,$

kjer je:

• $c \,$ neničelna realna konstanta

Katenoid dobimo tudi iz helikoida brez raztegovanja (glej animacijo na desni).

Viri

• Euler, Leonhard (1969). Methodus inveniendi lineas curvas maximi minimive propietate gaudeates sive solutio problematis isoperimetrici latissimo sensu accepti. Cambridge, MA: Harvard University Press. 

Zunanje povezave

• Verižnica in katenoid (v slovenščini)
• Katenoid na Mathworld (v angleščini)
• Različne oblike katenoidov (v angleščini)
• Spreminjanje katenoida v helikoid (z animacijo) (v angleščini)