Polpolieder

Polpolieder (tudi hemipolieder) je uniformni zvezdni polieder. Njegove stranske ploskve potekajo skozi njegovo središče. Te pol (»hemi«) stranske ploskve ležijo vzporedno z nekim drugim simetričnim poliedrom. Njihovo število je samo polovica stranskih ploskev tega drugega poliedra. Iz tega izhaja tudi predpona »hemi«.

Predpona »hemi« se uporablja tudi za določene projektivne poliedre kot je npr. polkocka, ki je slika preslikave 2 v 1 sfernega poliedra s centralno simetrijo.

Wythoffov simbol in slika oglišč

Wythoffovi simboli imajo obliko ^p/_(p − q) ^p/_q | r; njihove slike oglišč so križni štirikotnik|križni štirikotniki. Slika oglišč je enaka ^p/_q.2r.^p/_(p − q).2r. 2r-kotniške stranske ploskve tečejo skozi središče modela. Notacija ^p/_(p − q) vključuje {^p/_q} stranskih ploskev, ki se obračajo nazaj okoli slike oglišč.

Devet oblik skupaj s Wythoffovimi simboli je:

tetrahemiheksaeder 3/2 3 ǀ 2 (3.4.3/2.4) (p/q = 3, r = 2)	oktahemioktaeder 3/2 3 ǀ 3 (3.6.3/2.6) (p/q = 3, r = 3)	mali ikozihemidodekaeder 3/2 3 ǀ 5 (3.10.3/2.10) (p/q = 3, r = 5)	veliki ikozihemidodekaeder 3/2 3 ǀ 5/3 (3.10/3.3/2.10/3) (p/q = 3, r = 5/3)	mali dodekahemiikozaeder 5/3 5/2 ǀ 3 (5/2.6.5/3.6) (p/q = 5/2, r = 3)
	kubohemioktaeder 4/3 4 ǀ 3 (4.6.4/3.6) (p/q = 4, r = 3)	mali dodekahemidodekaeder 5/4 5 ǀ 5 (5.10.5/4.10) (p/q = 5, r = 5)	veliki dodecahemidodecahedron 5/3 5/2 ǀ 5/3 (5/2.10/3.5/3.10/3) (p/q = 5/2, r = 5/3)	veliki dodekahemiikozaeder 5/4 5 ǀ 3 (5.6.5/4.6) (p/q = 5, r = 3)

Orientabilnost

Samo oktahemioktaeder predstavlja orientabilno ploskev. Vsi ostali polpoliedri so neorientabilni ali ploskve s samo eno stranjo.

Dualna telesa polpoliedrov

Ker imajo polpoliedri stranske ploskve, ki potekajo skozi središče, imajo pripadajoče dualne oblike oglišča v neskončnosti ali na realni projektivni ravnini v neskončnosti . V knjigi Magnus Wenninger (rojen 1919) dualni modeli so prikazani kot sekajoče se prizme, ki so podaljšane v obeh smereh za isto sliko oglišč do neskončnosti, da bi se obdržala simetrija. V resnici se modeli prizem odrežejo v določeni točki, kar je ugodno za izdelovalce. Wenninger predlaga, da so te oblike nov razred stelacije, ki jo imenujemo stelacija v neskončnosti. Predlagal je tudi, da ta vrsta konstrukcije ne potrjuje običajnih definicij.

Obstoja devet takšnih dualov:

tetrahemiheksakron	oktahemioktakron in heksahemioktakron	mali ikozihemidodekakron in mali dodekahemidodekakron	veliki dodekahemidodekakron in veliki ikozihemidodekakron	veliki dodekahemiikozakron in mali dodekahemiikozakron
3 sekajoče se neskončne štiristrane prizme	4 sekajoče se neskončne šeststrane prizme	6 sekajoče se neskončne desetstrane prizme	6 sekajočih se neskončnih desetstranih prizem	10 sekajočih se neskončnih šeststranih prizem

Odnosi s kvazipravilnimi poliedri

Polpoliedri se pojavljajo v parih kot facetiranje kvazipravilnih poliedrov s štirimi stranskimi ploskvami na oglišču. Ti kvazipravilni poliedri imajo sliko oglišč m.n.m.n. Njihovi robovi tvorijo tudi n-kotne in m-kotne stranske ploskve, ki tvorijo polstranske ploskve polpoliedra. Tako se lahko polpolieder dobi iz kvazipravilnih poliedrov tako, da se zavrže m- in n-kotnike in se potem vpelje polstranske ploskve. Ker se je zavrglo m- in n-kotnike, se lahko vsakega od dveh polpoliedrov dobi iz kvazipravilnega poliedra. Tega pa se ne da narediti za oktaeder in tetraeder, kjer velja m = n = 3 in sta facetiranji skladni. Ta vrsta konstrukcije ne deluje za kvazipranevilne poliedre s šestimi stranskimi ploskvami na oglišču ker njihovi robovi ne tvorijo nobene pravilne polstranske ploskve.

Ker imajo polpoliedri tako kot kvazipravilni poliedri, ki imajo dve vrsti stranskih ploskev, ki se izmenoma pojavljajo okrog vsakega oglišča, se jih obravnava tudi kot kvazipravilne.

Kvazipravilni poliedri m.n.m.n	polstranske ploskve (h-kotniki)	polpoliedri z m-kotniki uporabljeni z m.h.m/m - 1.h	polpolieder z n-kotniki uporabljen z n.h.n/n - 1.h
tetratetraeder 3.3.3.3 m = 3, n = 3	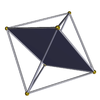kvadrati {4}	tetrahemiheksaeder 3.4.3/2.4	tetrahemiheksaeder 3.4.3/2.4
kubooktaeder 3.4.3.4 m = 3, n = 4	šestkotniki {6}	kubohemioktaeder 4.6.4/3.6	oktahemioktaeder 3.6.3/2.6
ikozidodekaeder 3.5.3.5 m = 3, n = 5	desetkotniki {10}	mali dodekahemidodekaeder 5.10.5/4.10	mali ikozihemidodekaeder 3.10.3/2.10
dodekadodekaeder 5.5/2.5.5/2 m = 5, n = 5/2	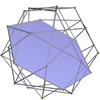šestkotniki {6}	mali dodekahemikozaeder 5/2.6.5/3.6	veliki dodekahemiikozaeder 5.6.5/4.6
veliki ikozidodekaeder 3.5/2.3.5/2 m = 3, n = 5/2	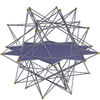dekagrami {10/3}	veliki dodekahemidodekaeder 5/2.10/3.5/3.10/3	veliki ikozihemidodekaeder 3.10/3.3/2.10/3

Tukaj m in n odgovarjata zgornjemu p/q in h pomeni 2r (glej zgoraj).