10-simpleks

Pravilni hendekaksenon (10-simpleks)
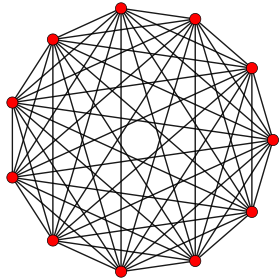Ortogonalna projekcija znotraj Petrijevega mnogokotnika
Tip	pravilni 10-politop
Družina	simpleks
Schläflijev simbol	{3,3,3,3,3,3,3,3,3}
Coxeter-Dynkinov diagram
9-stranskih ploskev	11 9-simpleks
8-stranskih ploskev	55 8-simpleks
7-stranskih ploskev	165 7-simpleks
6-stranskih ploskev	330 6-simpleks
5-stranskih ploskev	462 5-simpleks
4-stranske ploskve	462 5-celica
celice	330 tetraeder
stranske ploskve	165 trikotnik
robovi	55
oglišča	11
Slika oglišč	9-simpleks
Petrijev mnogokotnik	hendekagon
Coxeterjeva grupa	A10 [3,3,3,3,3,3,3,3,3]
dualnost	Sebi dualni
lastnosti	konveksni

10-simpleks je v geometriji sebi dualni pravilni 10-politop. Ima 11 oglišč, 165 trikotnih stranskih ploskev, 55 robov, 330 tetraederskih celic, 4 stranske ploskve, 462 5-celic s 4 stranskimi ploskvami, 5-simpleksov s 5 stranskimi ploskvami, 330 6-simpleksov z 6 stranskimi ploskvami, 165 7-simpleksov s 7 stranskimi ploskvami, 55 8-simpleksov z 8 osmimi stranskimi ploskvami in 11 9-simpleksov z 9 stranskimi ploskvami.

Diederski kot je cos⁻¹(1/10) ali okoli 84,26°.

Imenujemo ga tudi dendekaksenon ali dendeka-10-top kot politop z 11 facetami v 10 razsežnostih. Izraz hendekaksenon izvira iz grške besede hendeka, kar pomeni 11 facet in končnice -xenn (oblika besede ennea za devet), kar pomeni 9 razsežne facete ter končnice -on.

Koordinate

V kartezičnem koordinatnem sistemu so oglišča pravilnega 10-simpleksa, ki se nahaja v izhodišču, in ima rob dolg 2:

$\left(\sqrt{1/55},\ \sqrt{1/45},\ 1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ \sqrt{1/6},\ \sqrt{1/3},\ \pm1\right)$

$\left(\sqrt{1/55},\ \sqrt{1/45},\ 1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ \sqrt{1/6},\ -2\sqrt{1/3},\ 0\right)$

$\left(\sqrt{1/55},\ \sqrt{1/45},\ 1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ -\sqrt{3/2},\ 0,\ 0\right)$

$\left(\sqrt{1/55},\ \sqrt{1/45},\ 1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ \sqrt{1/15},\ -2\sqrt{2/5},\ 0,\ 0,\ 0\right)$

$\left(\sqrt{1/55},\ \sqrt{1/45},\ 1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ -\sqrt{5/3},\ 0,\ 0,\ 0,\ 0\right)$

$\left(\sqrt{1/55},\ \sqrt{1/45},\ 1/6,\ \sqrt{1/28},\ -\sqrt{12/7},\ 0,\ 0,\ 0,\ 0,\ 0\right)$

$\left(\sqrt{1/55},\ \sqrt{1/45},\ 1/6,\ -\sqrt{7/4},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)$

$\left(\sqrt{1/55},\ \sqrt{1/45},\ -4/3,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)$

$\left(\sqrt{1/55},\ -3\sqrt{1/5},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)$

$\left(-\sqrt{20/11},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)$.

10-simpleks lahko damo v 10-prostor kot permutacije (0,0,0,0,0,0,0,0,0,1). Ta vrsta konstrukcije je osnovana na facetah in 11-ortopleksu.

Slike 10-simpleksov

• 

  Coxeterjeva ravnina A₁₀, diederska simetrija [11].
• 

  Coxeterjeva ravnina je A₉, diederska simetrija je [10]
• 

  Coxeterjeva ravnina je A₈, diederska simetrija je [9]

• 

  Coxeterjeva ravnina je A₇, diederska simetrija je [8]
• 

  Coxeterjeva ravnina je A₆, diederska simetrija je [7]
• 

  Coxeterjeva ravnina je A₅, diederska simetrija je [6]

• 

  Coxeterjeva ravnina je A₄, diederska simetrija je [5]
• 

  Coxeterjeva ravnina je A₃, diederska simetrija je [4]
• 

  Coxeterjeva ravnina je A₂, diederska simetrija je [3]